1

INITIAL INQUIRY

Does this inequality have any solutions over the positive integers?

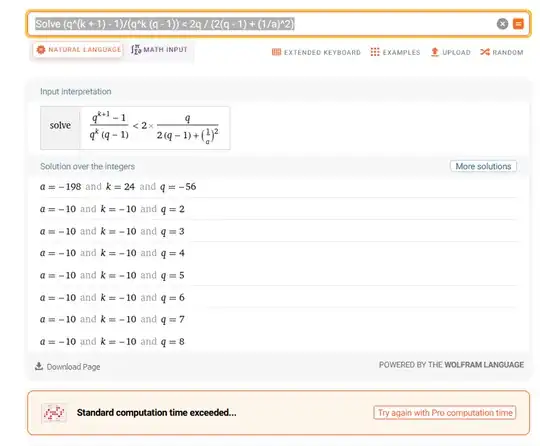
$$\dfrac{q^{k + 1} - 1}{q^k (q - 1)} < \dfrac{2q}{2(q - 1) + (1/a)^2}$$

I tried asking WolframAlpha for (some of) the solutions, it seems that there is no solution where all of $q, k$, and $a$ are positive integers.

Screenshot from WolframAlpha

MY ATTEMPT

Suppose that there exist $q, k, a \in \mathbb{Z}^{+}$ such that $$\dfrac{q^{k + 1} - 1}{q^k (q - 1)} < \dfrac{2q}{2(q - 1) + (1/a)^2}.$$

First, I noted that $$\dfrac{q^{k + 1} - 1}{q^k (q - 1)} < \frac{q}{q - 1}$$ and that $$\frac{q}{q - 1}$$ is the least upper bound of the set $$\mathscr{Q} = \{\dfrac{q^{k + 1} - 1}{q^k (q - 1)}\}.$$

In particular, I also noticed that $$\dfrac{2q}{2(q - 1) + (1/a)^2} < \frac{q}{q - 1}.$$

This contradicts the fact that $q/(q - 1)$ is the least upper bound of $\mathscr{Q}$.

Hence, the inequality $$\dfrac{q^{k + 1} - 1}{q^k (q - 1)} < \dfrac{2q}{2(q - 1) + (1/a)^2}$$ has no solutions where all of $q, k$, and $a$ are positive integers.

FINAL INQUIRY

Is my solution correct? If it is incorrect, how can the proof be mended so as to produce a valid argument?

Jose Arnaldo Bebita Dris
  • 8,471
  • 1
    The answer below is excellent, but I wanted to point out that if you add "in positive integers" or "over the positive integers" to the end of your query, you would have gotten a number of solutions, including $q=k=a=2$. (Note that $q=k=2, a \ge 2, a \in \mathbb{Z}$ works for all $a$.) WA looks for the easiest answers, unless you specifically tell it to stay in the positive. – Eric Snyder Jun 16 '22 at 08:30

1 Answers1

2

Actually there are infinitely many positive interger solutions.

Consider $q=2,k=1$ and $a\in\mathbb Z\cap[2,\infty)$, then $$\frac{q^{k+1}-1}{q^k(q-1)}=\frac32<\frac4{2+(1/2)^2}\leq\frac{2q}{2(q-1)+(1/a)^2}.$$

The issue in the proof: The left-hand side is $\frac{q-1/q^k}{q-1}$, so you are right that $\frac q{q-1}$ is the least upper bound for all $q>1,k>0$. But no matter how large $q$ is, there always exists some gap between $\frac{q-1/q^k}{q-1}$ and $\frac q{q-1}$, i.e. the interval $(\frac{q-1/q^k}{q-1}, \frac q{q-1})$ is non-empty, and the smaller the $q$ the larger the gap. On the other hand, the right-hand side $\frac{2q}{2(q-1)+(1/a)^2}$ can get arbitrarily close to $\frac q{q-1}$ if $a$ is sufficiently large, this means we can choose a small $q$ such that the gap $(\frac{q-1/q^k}{q-1}, \frac q{q-1})$ is big, and choose a large $a$ such that the right-hand side lies in this gap, i.e. $\frac{2q}{2(q-1)+(1/a)^2}\in(\frac{q-1/q^k}{q-1}, \frac q{q-1})$. By this idea, we can construct infinitely many positive integer solutions.

Mengchun Zhang
  • 2,995
  • 2
    And you needn't even choose a tiny $q$ or $k$; $a$ just gets vastly larger exponentially. For instance, for $q=k=10$, any $a \ge 90;000;000;001$ works. – Eric Snyder Jun 16 '22 at 08:33
  • @EricSnyder That's absolutely right, it should be that a is relatively larger than q,k. Thanks for the comment! – Mengchun Zhang Jun 16 '22 at 08:55