6

Is there a general way to determine the type of a knot given by a diagram? I am using KLO (Kirby calculator) and I encounter some nontrivial knots while doing this. For example, can we determine the type of the following diagram? 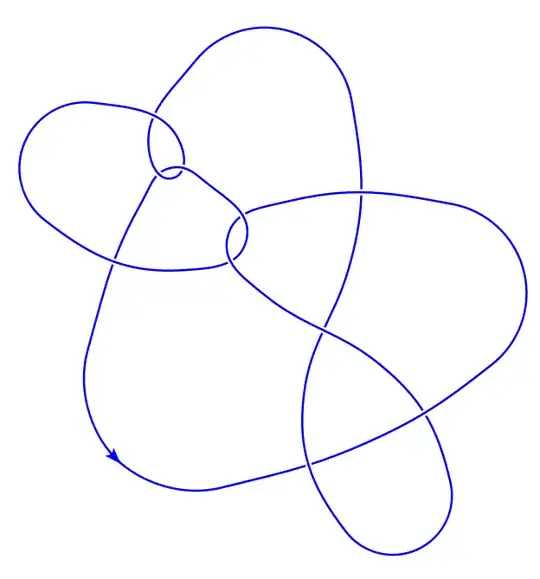enter image description here

user302934
  • 1,738
  • 1
  • 9
  • 27
  • 2
    In general this is a hard problem. The first job is to find the prime decomposition of your knot (this one looks prime to me). You given diagram gives an upper bound on the crossing number of the knot, so that bounds the search space you need to look in the knot tables. Next you can try computing various knot invariants to narrow down the options (eg Jones polynomial). This will give you a (hopefully very short) list of possible candidate knots. If this list contains more than 1 option you can try applying Reidemeister moves to get matching diagrams – David Sheard Jun 08 '22 at 14:12
  • 5
    There are indeed several knot recognition algorithms; see for example this MO link. But it's a very hard problem, perhaps the central problem of knot theory, and your question is not easy to answer in short order. – Lee Mosher Jun 08 '22 at 14:17
  • This diagram simplifies significantly with a few Reidemeister moves, after which it becomes alternating. Alternating knots are easy to classify. – Cheerful Parsnip Jun 08 '22 at 14:21
  • After simplifying, it looks like the knot is 8_1. – Cheerful Parsnip Jun 08 '22 at 14:28

3 Answers3

5

The best currently known algorithm for unknot recognition is due to Marc Lackenby, it runs in quasi-polynomial time $c^{\log c}$, where $c$ is the crossing number of the knot diagram. There is not (yet) a paper out, but Lackenby gave several talks on this in the last year or so (see Ian Agol's answer here for references). The oldest known algorithm for knot recognition (which has exponential run time) is due to Haken. It is implemented in SnapPy and Regina programs. Lackenby's algorithm is a very clever (and major!) improvement of Haken's idea. However, afaik, it is not yet implemented.

Moishe Kohan
  • 111,854
5

I pasted this diagram into KnotFolio, where it computes a few invariants like the Jones and Alexander polynomials. It has a database of all knots up to 10 or 11 crossings (courtesy of KnotInfo), and, assuming the knot is prime, the only possible knot is $8_1$.

The Alexander polynomial is reportedly $3t^2-7t+3$, which is irreducible, so if the knot were a connect sum one of the summands would have to have Alexander polynomial equal to 1. This is a ten crossing knot, so summands must have 3-7 crossings, and KnotInfo shows there are no such knots, so it is indeed prime.

KnotFolio also outputs the PD code for SnapPy, which we can ask to try to identify by looking for a homeomorphism of the knot exterior that is an isometry taking meridians to meridians (assuming the knot has a hyperbolic exterior). Using SnapPy in Sage:

sage: import snappy
sage: L=snappy.Link([(19,17,20,16), (17,12,18,13), (1,5,2,4),
....: (3,8,4,9), (20,7,1,8), (9,2,10,3), (10,15,11,16),
....: (14,6,15,5), (11,18,12,19), (6,14,7,13)])
sage: L.exterior().identify(True)
[m074(0,0), 8_1(0,0), K5_2(0,0), K8a11(0,0)]

SnapPy is indeed able to solve the gluing equations for a hyperbolic structure on L.exterior() (L.exterior().solution_type() gives "all tetrahedra positively oriented"), so 8_1 it is.

Kyle Miller
  • 20,247
2

If you have a diagram of a knot with no more than 16 crossings, then I found the following method the quickest.

Save your image of a diagram to a file. Upload it into https://kmill.github.io/knotfolio/ then copy the resulting DT code, and paste it into https://knotinfo.math.indiana.edu/homelinks/knotfinder.php then click Find.

knotMJ
  • 186
  • 3