I am completely lost on how to find cell structures on high dimensional manifolds such as $S^2×S^4$. The best I can do is try to generalize a procedure for low dimensional manifolds like $T^2=S^1×S^1$. I can imagine the prior structure as there being a copy of $S^4$ associated to each point of $S^2$, and this copy of $S^2$ can be a $2$-cell. I don't know if this is the correct way to even think about this or if I am on the right track with this. Also, is there a general method for even stranger things like $CP^n$?
1 Answers
There is a way to get a CW-structure for a product $X\times Y$ of compactly generated CW-complexes using their CW-structures. See e.g. Cartesian product of two CW-complexes. Then you can use that $S^n$ has the CW-structure given by a single $0$-cell and a single $n$-cell. This gives a CW-structure on $S^n\times S^m$.
I don't think there is a general way to find a CW-structure for a space $X$ which has a $CW$-structure. However, it is not difficult to find a homotopy equivalent space with a CW-structure. Namely there is a way to construct a weak homotopy equivalence $Z\to X$ for any space $X$ where $Z$ is a CW-complex with an explicitly constructed CW-structure, and in the case where $X$ is as CW-complex, it will then be a homotopy equivalence by the Whitehead theorem. This construction can be seen in for example Hatcher's book in the section on CW-approximations.
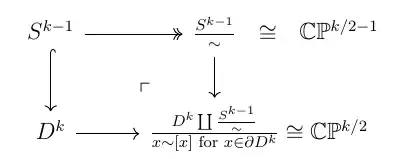
Let me also give a nice descriptions of a CW-structure for $\mathbb{C}P^n$. First, we note that $\mathbb{C}P^n\cong \frac{S^{2n+1}}{\sim}$ where $\sim$ is the relation given by $z\sim w$ if there exists $t\in \mathbb{C}$ with $|t|=1$ such that $z=tw$ where $S^{2n+1}$ is considered as a subspace of $\mathbb{C}^{n+1}$.Then $\mathbb{C}P^n$ has a CW-structure with a single $k$-cell for each even $k$ satisfying $0\leq k \leq 2n$ with gluings given by the pushout diagrams:
In other words one can get $\mathbb{C}P^{n}$ by gluing a $2n$-cell to $\mathbb{C}P^{n-1}$ via the attaching map $S^{2n-1}\to \frac{S^{2n-1}}{\sim}\cong \mathbb{C}P^{n-1}$.
- 1,199
-
Thank you so much for the in-depth answer. When it comes to describing the (co)homology of $\mathbb{CP}^n$, is it true that the boundary maps all cells to $0$ as there are no cells in every alternating dimension so $H_{2m}(X^{2m},X^{2m-1})=\mathbb{Z}$ and $H_{2m+1}(X^{2m+1},X^{2m})=0$? – Sam Gue Jun 07 '22 at 22:22
-
1Yes, that is correct for $m\leq n$. – Frederik Jun 07 '22 at 22:35