7

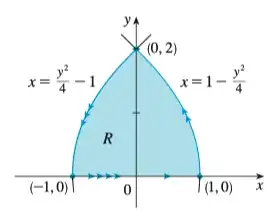
Use the change of variables $x=u^2-v^2$, $y=2uv$ to evaluate $$\iint_{R}y dA$$ where $R$ is the region bounded by the x-axis, the parabolas $y^2=4-4x$ and $y^2=4+4x, y\geq0$

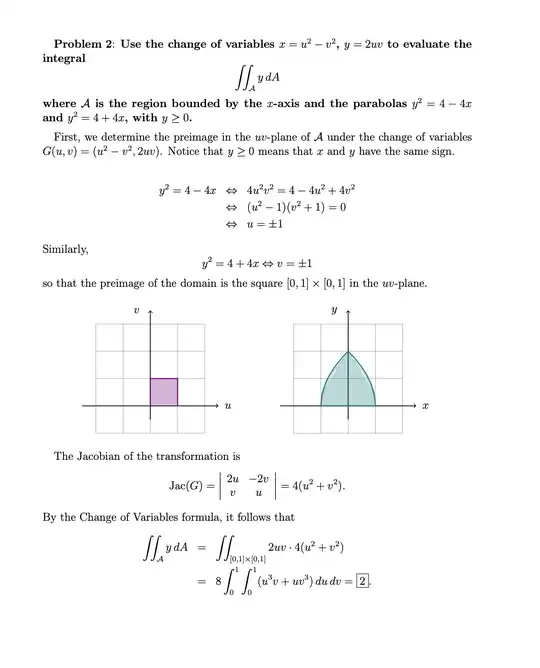
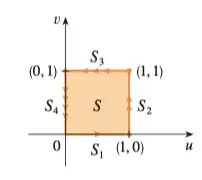
I'm following along with this solution: enter image description here

I don't understand why the preimage of the domain is $[0,1]\times [0,1]$

I understand how we get $u=\pm 1$ and $v=\pm 1$ but I don't know how the bounds are from $0$ to $1$?

Why isn't it $$\int_{-1}^{1}\int_{-1}^{1} 2uv(4u^2+4v^2)dudv$$

EDIT: verify that there is some typo for the Jacobian, Because it should be

$\begin{vmatrix} 2u & -2v \\ 2v & 2u \end{vmatrix}=4(u^2+v^2)$

RobPratt
  • 50,938
user8290579
  • 914
  • 2
    Your book has a misprint, it should say "$y \ge 0$ means that $u$ and $v$ have the same sign" – WW1 Jun 06 '22 at 22:19
  • 1
    Okay so are the bounds from $0$ to $1$ correct? Because I still don't understand how it's just the area from 0 to 1. Shouldn it essentially include the 1st quadrant and the 3rd quadrant? – user8290579 Jun 06 '22 at 22:25
  • 2
    Both of those squares in the $uv$ plane map onto the entire region in the $xy$ plane - you can use one or the other, but not both. – WW1 Jun 06 '22 at 22:37

1 Answers1

4

It may be helpful to break the boundary of $R$ into four pieces and look at their preimages:

enter image description here enter image description here

Since $y=2uv$ and $y\ge 0$ imply that $u$ and $v$ must have the same sign, you could either use $[0,1]\times[0,1]$ or $[-1,0]\times [-1,0]$, but not both because you need the transformation to be one-to-one in order to calculate the double integral.

[Added.] Note that the mapping $G(u,v)=(u^2-v^2,2uv)$ is not injective: $G(u,v)=G(-u,-v)$. In order to use it in the double integral, one should restrict its domain to a subset of $\mathbf{R}^2$ in order to get an injection. For instance, $\{(u,v):v\ge 0\}$.

Now, consider $$ R_2=\{(x,y): 0\le y\le 2,\quad x=1-\frac{y^2}{4}\} $$ The second condition in terms of $(u,v)$ is $$ x=1-\frac{y^2}{4}\Longleftrightarrow u^2-v^2=1-u^2v^2 \Longleftrightarrow (u^2-1)(v^2+1)=0 \Longleftrightarrow u^2=1\tag{1} $$ The first condition $$ 0\le y\le 2 \Longleftrightarrow 0\le 2uv \le 2 \Longleftrightarrow 0\le uv\le 1\tag{2} $$ Combining (1) and (2) together you get that the preimage of the piece $R_2$ is $$ S_2=\{(u,v): u=1, 0\le v\le 1\}. $$

You can similarly figure out how to get the preimage of the other pieces.

  • could you please explain how you go from the image on the left to the image on the right? I'm quite confused on what numbers you need to plug in so that the boundaries turn in the left graph turn into a square in the right graph? – user8290579 Jun 06 '22 at 22:57
  • okay, I think I understand partly what you are saying. So essentially I can have two squares of size 1. one of them will be in the first quadrant and the other will be in the third quadrant right? But then Why am I not doing 2 times the double integral from 0 to 1 of the region? – user8290579 Jun 06 '22 at 23:23
  • "So essentially I can have two squares of size 1" This is not correct. You only have one square, because the transformation $G$ must be injective. –  Jun 06 '22 at 23:33
  • @user8290579 see edits. –  Jun 07 '22 at 00:09