Can I prove that $f$ convex $\implies$ $f$ continuous using a proof by all possible cases of discontinuity, showing contradiction in each one?

Question

Given the following definitions of a convex function from Spivak's Calculus:

Definition 1: A function $f$ is convex on an interval, if for all $a$ and $b$ in the interval, the line segment joining $(a,f(a))$ and $(b,f(b))$ lies above the graph of $f$.

Definition 2: A function $f$ is convex on an interval if for all $a, x$, and $b$ in the interval with $a<x<b$ we have $\frac{f(x)-f(a)}{x-a}<\frac{f(b)-f(a)}{b-a}$.

First question: Does Definition 2 mean that $f$ has to be defined everywhere in an interval to be convex in that interval?

Second question: Is it possible to prove that such a function is always continuous? If so, how?

Here is my attempt at a proof. I'm going to outline the proofs, without actually proving using $\epsilon$ and $\delta$ proofs as would be required to be rigorous. If the general idea of each case below is sound, then I think the corresponding rigorous proofs are relatively simple.

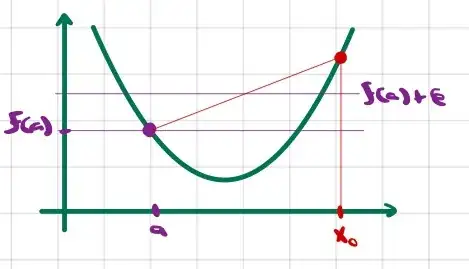
Let $f$ be convex. Assume $f$ is discontinuous at some point $a$, ie $\lim\limits_{x \to a} f(x) \neq f(a)$.

My proof strategy is to go through each of the possible ways that $f$ could be discontinuous at $a$ and show that they violate convexity of $f$.

Removable discontinuities aren't possible if $f$ must be defined at every point in an interval to be convex.

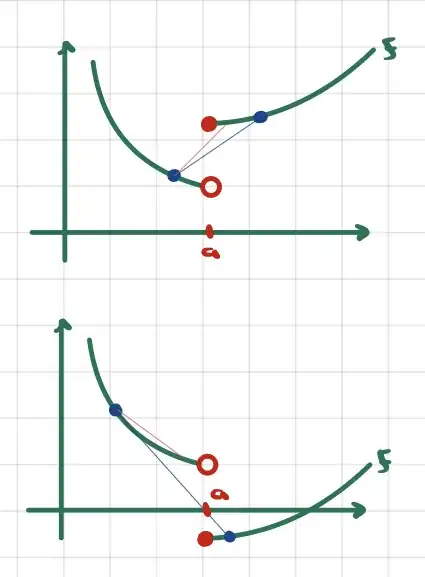
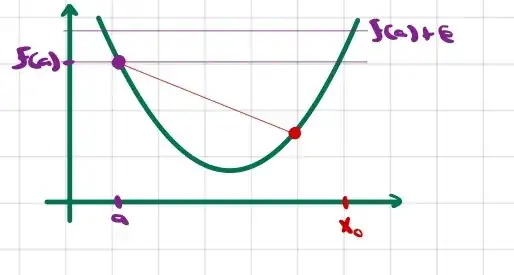
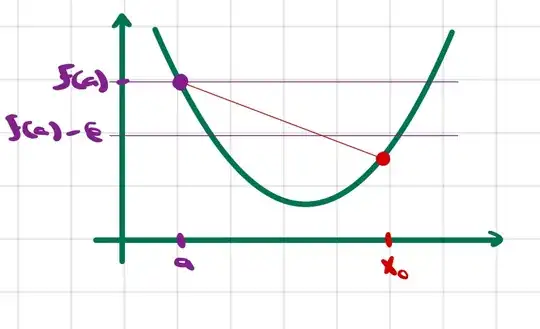
Jump discontinuities aren't possible for a convex function, due to the following two situations:

In both cases above, the light red line has a slope that is larger than the slope of the blue line, and this violates convexity.

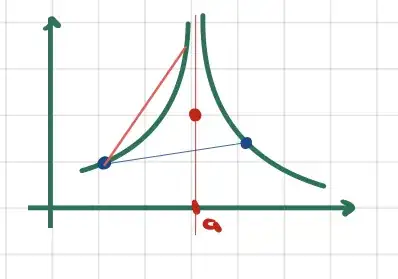
Essential discontinuities aren't possible because the slope between any point $x_1<a$ and a point $a+h$ can be made arbitrarily high. Just choose an $h_1>0$ and an $h_2<0$, let the slope between $x_1$ and $a+h_1$ be some value. Then we can always find an $a+h_2$ with a larger slope, violating convexity as in the picture below.

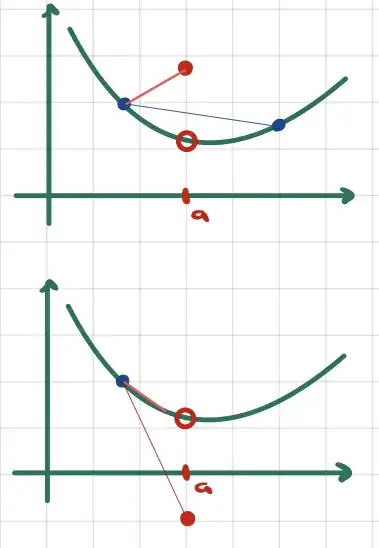
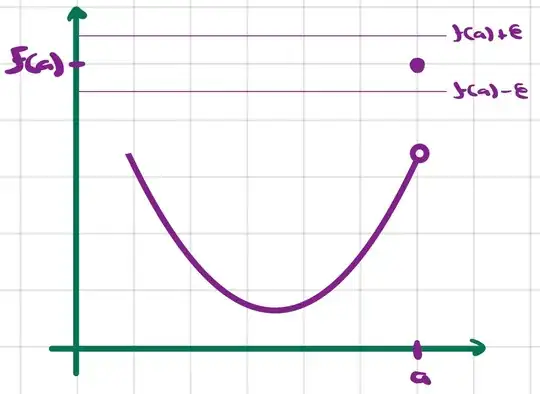
Finally, consider the case of a point discontinuity

Whether $f(a)>\lim\limits_{x \to a} f(x)$ or $f(a)<\lim\limits_{x \to a} f(x)$, convexity is violated.

In all possible cases, $f$ turns out not to be convex, a contradiction.

Therefore, by proof by contradiction, we conclude that $f$ must be continuous at every point.

Is this approach (proof by possible cases of discontinuity, showing contradiction in each one) correct?

Answer 1

Here is a proof that if $f$ is convex on $\mathbb{R}$ or any open interval then $f$ is continuous (Problem 10, chapter 11 Appendix, "Convexity and Concavity", Calculus by Spivak)

Proof

We want to show that $\lim\limits_{x \to a} f(x)=f(a)$. We can do this by showing that for any $\epsilon>0$ there is always an interval around $a$ in which $|f(x)-f(a)|<\epsilon$.

First we show $f(x)-f(a)<\epsilon$ then we show $-\epsilon<f(x)-f(a)$.

Let $x_0>a$.

The line segment from $(a,f(a)$ to $(x_0,f(x_0)$ is

$$g(x)=f(a)+\frac{f(x_0)-f(a)}{x_0-a}, x \in [a,x_0]\tag{1}$$

$$g(x)<f(x)+\epsilon \implies (f(x_0)-f(a))(x-a)<\epsilon(x_0-a)$$

Case 1: $f(x_0)>f(a)$

$$x<a+\epsilon\frac{x_0-a}{f(x_0)-f(a)}=\alpha$$

Since $g(a)=f(a)$ and $\forall x, x \in (a, x_0) \implies f(x)<g(x)$ (because $f$ is convex), then for $x \in (x_0, min(x_0, \alpha))$ we have $f(x)<f(a)+\epsilon$.

Case 2: $f(x_0)<f(a)<f(a)+\epsilon$

Now let $x_0<a$.

Again we have $(1)$

Case 1: $f(x_0)>f(a)$

$$(f(x_0)-f(a))(x-a)>\epsilon(x_0-a)$$

Note that now we have a $>$ because $x_0-a<0$.

Then $x>a+\epsilon\frac{x_0-a}{f(x_0)-f(a)}=\beta$, and note that $\beta<a$.

Since $g(a)=f(a)$, and $\forall x, x \in (x_0,a) \implies f(x)<g(x)$ (because $f$ convex), then for $x \in (max(x_0, \beta), a)$, we have $f(x)<f(a)+\epsilon$.

Therefore, at this point, for any $\epsilon>0$ there is an interval around $a$ such that $f(x)<f(a)+\epsilon$.

Now let's consider where $f(x)>f(a)-\epsilon$.

Let $x_0>a$.

Case 1: $f(x_0)>f(a)>f(a)-\epsilon$

Case 2: $f(x_0)<f(a)$

We start again with the equation for the line segment $(1)$.

$$g(x)>f(a)-\epsilon \implies x<a-\epsilon\frac{x_0-a}{f(x_0)-f(a)}=\alpha$$

Therefore

$$\forall x, x \in (a, min(x_0, \alpha)) \implies f(x)>f(a)-\epsilon$$

Finally we need to let $x_0<a$ and consider two final cases. I won't do them here, as they are totally analogous to the work shown above.

In the end we have shown that for any $\epsilon>0$ we can always find an interval around $a$ where $|f(x)-f(a)|<\epsilon$.

Why is the assumption of open interval important?

Let's say we had convexity on $[a,b]$. The proof above is correct to show continuity on interior points of $[a,b]$, that is points for which there are always other points in the interval that are larger than it.

However consider the following situation

This function is convex on a closed interval, even with the discontinuity at $a$. There is some $\epsilon>0$ such that we can't keep $f(x)$ within $(f(a)-\epsilon, f(a)+\epsilon)$ for $x$ sufficiently near $a$.