14

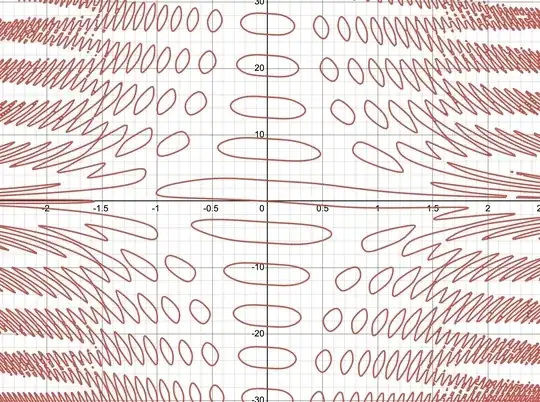
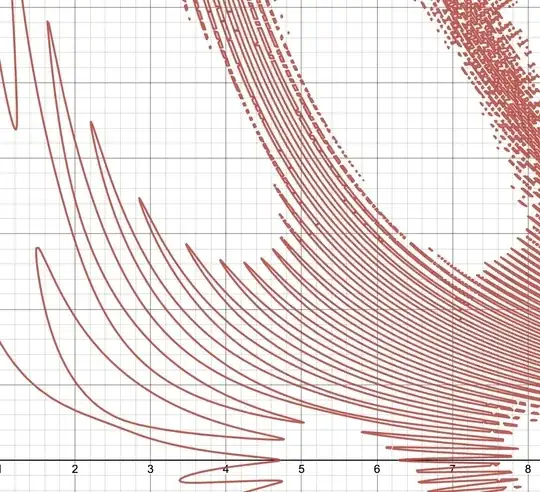
The graph of $\cos\left(x\right)-\sin\left(x+y\right)=\cos\left(x^{2}y\right)$ is, perhaps unsurprisingly, pretty wild. Here is a Desmos version of it; a few screenshots are below, showing different scales of the graph. As can be seen, for small values of $x$ (say $-1.5 \le x \le 1.5$) the graph consists of individual simple closed loops; this pattern persists as you move up and down the $y$-axis, although the loops become smaller and more squished together.

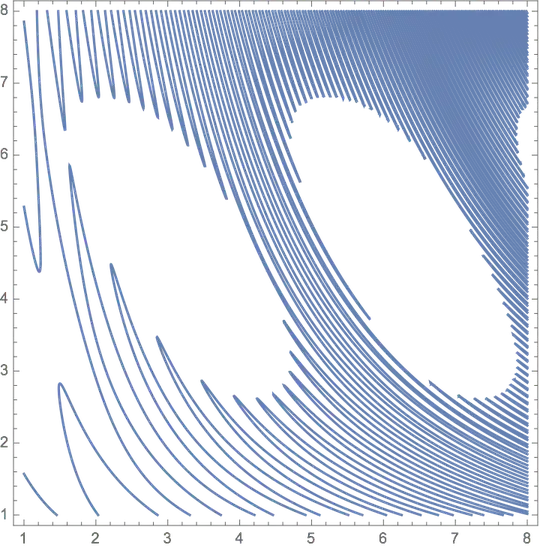
enter image description here

However, for larger values of $x$, the loops merge together into what appears to be a single enormous zig-zag pattern. What appear in this image to be isolated points are actually an artifact of Desmos's inability to resolve the fine details; zooming in more closely reveals that they are actually connected. This raises the provocative question: how much of this function is actually connected?

enter image description here

My question is: are there any techniques that can be used to describe the connected components of this wild graph? For example, if everything with $x > 5$ path-connected?

orangeskid
  • 56,630
mweiss
  • 24,547

1 Answers1

-1

Here is a plot in Mathematica ContourPlots with high resolution:

enter image description here

While each contour will be continuous (i.e., no isolated points as we see in the OP's plot), there may indeed be unconnected contour segments.

David G. Stork
  • 30,409
  • 2
    The solution set to an equation $F(x,y)=0$ need not be connected even if $F(x,y)$ is continuous. So continuity is insufficient to deduce connectedness. – Cheerful Parsnip May 23 '22 at 03:13
  • 1
    For example the solution set to $xy=1$ is disconnected. – Cheerful Parsnip May 23 '22 at 03:14
  • @CheerfulParsnip That's exactly the example I was about to provide: the graph of $xy = 1$ has two connected components. Continuity and connectedness are two different things! And the graph I asked about is clearly disconnected near the $x$-axis. – mweiss May 23 '22 at 03:39
  • 4
    Thanks for providing a neater graphical representation but "easy to see" is not the same a mathematical proof. – Jean Marie May 23 '22 at 04:47