Can a inscribed triangle divide a circle into 4 integer parts?

Question

Question

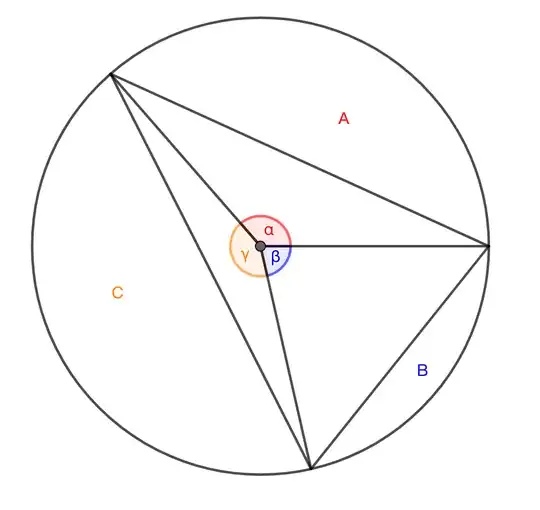
Draw an inscribed triangle on a circle and divide the circle into four parts $A, B, C, D$.

Can the areas of these parts be integers?

My attempt

Find the area of the arc from the central angle $(\alpha, \beta, \theta)$

$$ \begin{aligned} S &= π r^2\\ A &= \frac{r^2}{2}(\alpha-\sin\alpha)\\ B &= \frac{r^2}{2}(\beta-\sin\beta)\\ C &= \frac{r^2}{2}(\gamma-\sin\gamma)\\ \end{aligned} $$

with constraints

$$ \begin{aligned} S &= A+B+C+D\\ 2π &= \alpha + \beta + \gamma\\ \end{aligned} $$

which can expand to

$$ π r^2 = \frac{r^2}{2}(\alpha-\sin\alpha) + \frac{r^2}{2}(\beta-\sin\beta)+\frac{r^2}{2}(2π - \alpha - \beta-\sin(2π - \alpha - \beta))+D $$

and then simplify as

$$ D=\frac{r^2}{2}(4 \pi -2 (\alpha +\beta )+\sin (\alpha +\beta )+\sin (\alpha )+\sin (\beta )) $$

so, for $\pi>\beta \geqslant \alpha > 0$, $r\in\mathbb{R}_+$ have relation

$$ \begin{aligned} A &= \frac{r^2}{2}(\alpha-\sin\alpha)\\ B &= \frac{r^2}{2}(\beta-\sin\beta)\\ C &= \frac{r^2}{2}(2 \pi - (\alpha +\beta )+\sin(\alpha +\beta)\\ D &=\frac{r^2}{2}(4 \pi -2 (\alpha +\beta )+\sin (\alpha +\beta )+\sin (\alpha )+\sin (\beta ))\\ \end{aligned} $$

Looks like both have the form $p\pi - q$, if 4-parts are all rational numbers after removing this common factor, then you can adjust $r$ to make the four parts are integers.

I don't know how to find a integer solution or explain no solution.

Answer 1

Not an answer, just some thoughts.

Note you can rephrase the question in the unit disk, asking for a triangle with the ratios of the areas rational. If such a triangle exists, you can scale the circle and triangle to get integer areas, and visa verso.

In the unit disk, you get that the areas must be rational multiples of $\pi.$

If $f(x)=x-\sin x,$ this means you need $\alpha,\beta$ with $f(\alpha),f(\beta),f(\alpha+\beta)$ all rational multiples of $\pi.$

There are, of course, the degenerate case where $\alpha=\beta=\pi,$ or more generally, when $\alpha$ and $\beta$ are integer multiples of $\pi.$

Unfortunately, the $f$ is difficult to characterize in terms of number theory. Specifically, the set $S=f^{-1}(\pi\mathbb Q)$ is difficult to characterize. Certainly, $S$ doesn’t include any rational multiples of $\pi,$ other than the integer multiples of $\pi,$ the degenerate cases.

If you can’t find a nice property of $f,$ there is certainly no reason to expect to find non-degenerate angles with $\alpha,\beta,\alpha+\beta\in S,$ since $S$ is countable.