Question on term of derived formula for $\log\zeta(s)$

Question

The derived formula

$$\log\zeta(s)=-\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N 1_{n\in\mathbb{P}} \left(2 \tanh ^{-1}\left(1-2 n^s\right)-i \pi\right)\right),\quad s>1\tag{1}$$

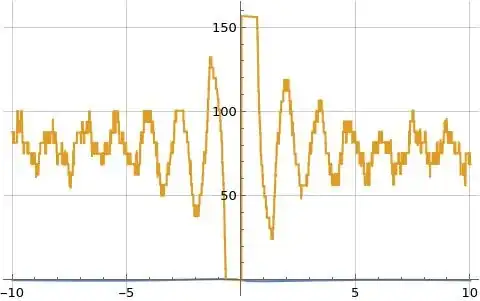
seems to converge for $s>1$ as illustrated in Figure (1) below, and the real part seems to converge for $\Re(s)>1\land \Im(s)\ne 0$ as illustrated in Figure (2) below, but the branch cuts of $\tanh^{-1}(z)$ cause problems when evaluating the imaginary part for $\Re[s]>1\land \Im(s)\ne 0$ as illustrated in Figure (3) below.

---

The problematic branch cuts of $\tanh^{-1}(z)$ can be compensated for as follows

$$\log\zeta(s)=-\underset{N\to\infty}{\text{lim}}\left(\sum _{n=1}^N 1_{n\in\mathbb{P}} \left(2 \tanh^{-1}\left(1-2 n^s\right)+i \pi \left( \begin{array}{cc} \{ & \begin{array}{cc} \begin{array}{cc} \{ & \begin{array}{cc} 1 & \Im\left(1-2 n^s\right)<0 \\ -1 & \text{Otherwise} \\ \end{array} \\ \end{array} & \Re\left(1-2 n^s\right)<-1 \\ \begin{array}{cc} \{ & \begin{array}{cc} -1 & \Im\left(1-2 n^s\right)>0 \\ 1 & \text{Otherwise} \\ \end{array} \\ \end{array} & \Re\left(1-2 n^s\right)>+1 \\ \begin{array}{cc} \{ & \begin{array}{cc} 1 & \Im\left(1-2 n^s\right)<0 \\ -1 & \text{Otherwise} \\ \end{array} \\ \end{array} & \text{Otherwise} \\ \end{array} \\ \end{array} \right)\right)\right),\quad\Re(s)>1\tag{2}$$

which is illustrated in Figure (4) below.

---

Question: Can the term in formula (2) above be expressed in terms of one or more standard functions which eliminate the need for the ugly piecewise expression contained in formula (2) above?

---

The prime indicator function $1_{n\in\mathbb{P}}$ in formulas (1) and (2) above returns $1$ if n is a prime number and $0$ otherwise. Consequently formulas (1) and (2) above are sums over the primes whereas the corresponding Dirichlet series

$\log\zeta(s)=\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N \frac{1}{n^s} 1_{n=p^k}\right),\quad\Re(s)>1\tag{3}$

is a sum over the prime-powers.

---

Formulas (1) and (2) above were derived from formula (4) below

$$\frac{\zeta'(s)}{\zeta(s)}=-\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N \frac{\log(n)}{n^s-1} 1_{n\in\mathbb{P}}\right),\quad\Re(s)>1\tag{4}$$

which is also a sum over the primes whereas the corresponding Dirichlet series

$$\frac{\zeta'(s)}{\zeta(s)}=-\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N \frac{\log(p)}{n^s} 1_{n=p^k}\right),\quad\Re(s)>1\tag{5}$$

is a sum over the prime-powers.

---

Here's another interesting formula related to formulas (1) and (4) above

$$C(s)=\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N \frac{\log(n)}{\left(n^s+n^{-s}\right)-2} 1_{n\in\mathbb{P}}\right),\quad\Re(s)>1\tag{6}$$

which provides an alternative way to evaluate the corresponding Dirichlet series

$$C(s)=\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N \frac{\log(n)}{n^s} 1_{n=p^k}\right),\quad\Re(s)>1\tag{7}$$

Note formula (6) above actually converges for $|\Re(s)|>1$ but only represents the function $C(s)$ defined in formula (7) above for $\Re(s)>1$.

---

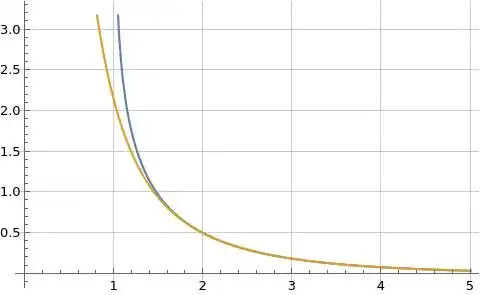
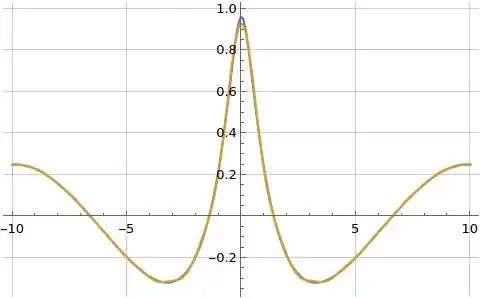
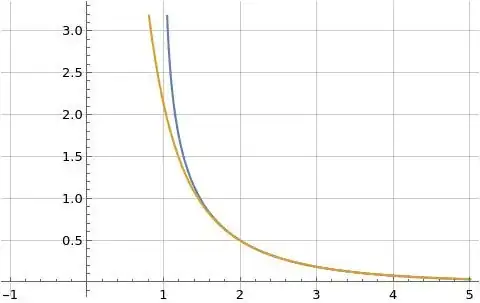
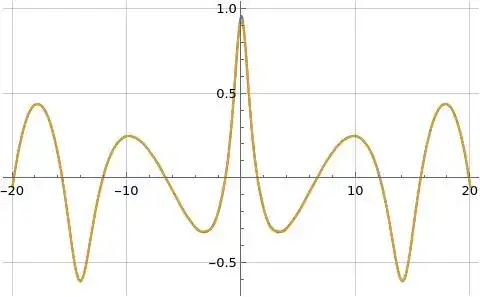
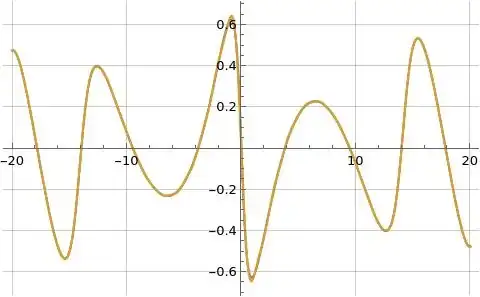
Figures (1), (2), and (3) below illustrate formula (1) for $\log\zeta(s)$ in orange overlaid on the blue reference function where formula (1) is evaluated at $N=100$.

---

Figure (1): Illustration of formula (1) for $\log\zeta(s)$ for real $s$

---

Figure (2): Illustration of real part of formula (1) for $\log\zeta(s)$ evaluated along the line $s=\frac{3}{2}+i t$

---

Figure (3): Illustration of imaginary part of formula (1) for $\log\zeta(s)$ evaluated along the line $s=\frac{3}{2}+i t$

---

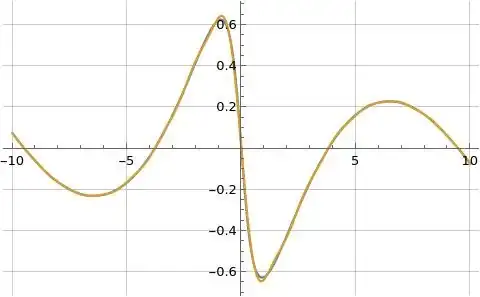
Figure (4) below illustrates the imaginary part of formula (2) for $\log\zeta(s)$ evaluated along the line $s=\frac{3}{2}+i t$ in orange overlaid on the blue reference function where formula (2) is evaluated at $N=100$.

---

Figure (4): Illustration of imaginary part of formula (2) for $\log\zeta(s)$ evaluated along the line $s=\frac{3}{2}+i t$

Answer 1

I've determined

$$\log\zeta(s)=-\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=2}^N 1_{n\in\mathbb{P}}\, \log\left(1-n^{-s}\right)\right),\quad \Re(s)>1\tag{1}$$

is a simpler and more correct formula which eliminates the problems with branch cuts associated with the formula in my question.

---

Figure (1) below illustrates formula (1) for $\log\zeta(s)$ above overlaid on the blue reference function where formula (1) is evaluated at $N=100$.

---

Figure (1): Illustration of formula (1) for $\log\zeta(s)$

---

Figures (2) and (3) below illustrate the real and imaginary parts of formula (1) for $\log\zeta(s)$ above evaluated along the line $s=\frac{3}{2}+i t$ overlaid on the blue reference function where formula (1) is evaluated at $N=100$ for both figures.

---

Figure (2): Illustration of real part of formula (1) for $\log\zeta(s)$ evaluated along the line $s=\frac{3}{2}+i t$

---

Figure (3): Illustration of imaginary part of formula (1) for $\log\zeta(s)$ evaluated along the line $s=\frac{3}{2}+i t$