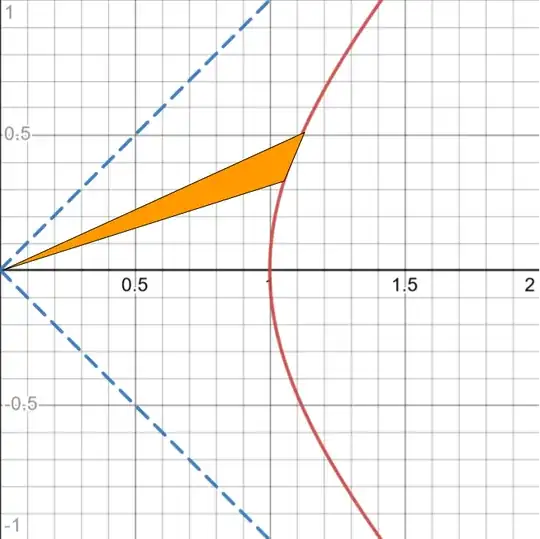
This question may be the closest to what I'm looking for, but the link in the answer uses a CAS to complete the proof. I was thinking I could derive the formulas for $\sinh{x}$ and $\cosh{x}$ using a very simple picture to get the differential equations. I've pasted the picture here. This is the unit hyperbola $x^2 - y^2 = 1$, so we know the coordinates are $(\cosh{A}, \sinh{A})$. The orange slice is $\frac12 dA$ (since $A$ is two-sided), and as you can see it has an area of $\frac12 dA = \frac12 x\ dy$. But that means $\frac{dy}{dA} = \frac1{x}$, whereas we know we want $\frac{dy}{dA} = x$, since $y$ and $x$ are the hyperbolic functions. How am I getting this backwards when it seems so simple?
-
Your triangle area is not correct. I am not at all convinced that $\mathrm{d}A=x,\mathrm{d}y$. Do you want a post explaining the calculus quadrature of the hyperbola, i.e. the usual derivation, or one showcasing a differential equation of the style you're going for? – FShrike May 02 '22 at 15:00
-
@FShrike Ooooh, now that you say that I can see it. Could you post whichever one leans more toward geometric intuition/visual approach? Thank you! – Adam Herbst May 02 '22 at 15:18
2 Answers
Let's be a little more careful with our differentials. The base of this triangle is a segment of length $\sqrt{dx^2+dy^2}$. This base is not vertical. It has a slope of $dy/dx$. Thus the altitude is not $x$, but $(x dy-ydx)/\sqrt{dx^2+dy^2}$. So the area is $(x dy - y dx)/2$, and we have the correct expression for $dA$: $$ dA = x dy - y dx. $$ This is actually a general statement for integrating areas inside curves like this. It's also a restatement of the fact that the area of a triangle is equal to half the cross product of two of its sides.
To get the specific relation between $dy$ and $dx$, we implicitly differentiate the hyperbola to get $x dx = y dy$. Then we can solve for $dy/dA$: $$ 1 = \left(x - \frac{y^2}{x}\right)\frac{dy}{dA} = \frac{1}{x}\frac{dy}{dA}\Longrightarrow \frac{dy}{dA} = x. $$ A similar calculation yields $dx/dA = y$, as expected.
- 23,253
$\newcommand{\d}{\mathrm{d}}$Let's bear in mind that the hyperbolic parameter, or the hyperbolic "angle", is defined to be twice the area measured from the axis.
Consider the "base" of your differential pseudo-triangle in orange, lying along the arc. This element is, loosely speaking, equal to: $$\sqrt{\d x^2+\d y^2}=\sqrt{1+\left(\frac{\d y}{\d x}\right)^2}\,\d x$$ But what is the "perpendicular height" of this triangle? Implicitly differentiate: $$x^2-y^2=1\implies 2x-2y\cdot\frac{\d y}{\d x}=0\\\implies\frac{\d y}{\d x}=\frac{x}{y}$$So the normal gradient is $-\frac{y}{x}$. Let's fix $(x_0,y_0)$ on the hyperbola. The normal to the hyperbola at that point is then: $$y=y_0-\frac{y_0}{x_0}(x-x_0)$$We can find the height by intersecting this line with the ray from the origin, of gradient equal to the tangent to the curve: $$y=\frac{x_0}{y_0}x$$These intersect when: $$x=\left(\frac{x_0}{y_0}+\frac{y_0}{x_0}\right)^{-1}\left(y_0+\frac{y_0}{x_0}x_0\right)=\frac{2y_0^2x_0}{x_0^2+y_0^2}\\y=\frac{2y_0x_0^2}{x_0^2+y_0^2}$$We compute the distance from this point to $(x_0,y_0)$ to find the height: $$h=\sqrt{\left(\frac{x_0(x_0^2+y_0^2)-2x_0y_0^2}{x_0^2+y_0^2}\right)^2+\left(\frac{y_0(x_0^2+y_0^2)-2y_0x_0^2}{x_0^2+y_0^2}\right)^2}\\=\sqrt{\frac{x_0^2}{(x_0^2+y_0^2)^2}(x_0^2-y_0^2)^2+\frac{y_0^2}{(x_0^2+y_0^2)^2}(y_0^2-x_0^2)^2}\\=\frac{|x^2_0-y^2_0|}{x_0^2+y_0^2}\sqrt{x_0^2+y_0^2}\\=\frac{1}{\sqrt{x_0^2+y_0^2}}$$The orange triangle then has area "base" (arc length) times "height" over $2$ which equals: $$\frac{1}{2}\frac{1}{\sqrt{x_0^2+y_0^2}}\sqrt{1+\frac{x_0^2}{y_0^2}}\,\d x\\=\frac{1}{2|y_0|}\d x$$Remembering the scale by two and insisting on a positive hyperbolic angle, we get the loose differential relation ($\alpha=2A$ the hyperbolic angle): $$\d\alpha=\frac{1}{y(x)}\d x=\frac{1}{\sqrt{x^2-1}}\d x$$Which, if you accept $x=\cosh\alpha$ as the definition, yields $\cosh\alpha=\frac{1}{2}(e^x+e^{-x})$ using standard techniques.
- 46,840
- 3
- 35
- 94