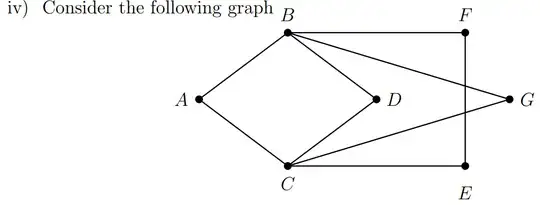
I can see intuitively why this graph will not have a Hamilton path, but I can't seem to write up a convincing proof. Are there any tips on how to prove that a graph does not have a hamilton path?
2 Answers
Assume for a contradiction that the graph has a Hamilton path $P$.
At least one of the three vertices $A$, $D$, $G$ is not an endpoint of $P$. By symmetry we may assume that $A$ is an internal point of $P$. Thus the edges $AB$ and $AC$ belong to $P$.
If vertex $D$ or $G$ were also an internal point of $P$, then $P$ would contain a cycle of length $4$, which would be absurd. Therefore, $D$ and $G$ must be endpoints of $P$.
Since a path has only two endpoints, $E$ and $F$ must be internal points of $P$. But then the edges $CE$, $EF$, and $BF$ must belong to $P$, so that $P$ contains a cycle of length $5$, which is absurd.
- 82,298
Consider the vertices $\{A, D, G\}$.
Consider the first vertex we arrive at which is one of these 3, WLOG assume it is $A$ (the graph is symmetric). To leave $A$, one must go through either $B$ or $C$, as the graph is symmetric, suppose it is $C$.
Later on, we must traverse the another from this set, say $D$, once again this is allowed by symmetry. There are two possible ways this may work.
We can immediately go to the next vertex in the set using the edge $CD$, and then leave $D$ with the only available choice of $DB$. But now it is easy to see that we cannot both reach $F$ and $G$, as arriving at one will trap us from arriving at the other.
There is some sort of detour, so that the edge $CD$ is not used. $C$ is already colored (from when we traversed $A$), so we must enter through $B$, but now we are trapped, as both exit routes $B$ and $C$ are already traversed, and we still have yet to traverse the remaining member of the set, so this cannot be the end.
And so it is impossible to construct such a path.
- 1,613