Only as regards the second question.
It is known that, for $n\ge 17$,
$$\frac{n}{\log n}\lt\pi(n)\lt\frac{1.25506\space n}{\log n}$$
Therefore, defining $S^*=S-\{4,16\}$ and assuming that (see my other question)
$$\sum_{n\space\in\space S^*}\frac{1}{n}=\frac{1}{e}-\frac{1}{16}\sim 0.30538$$
we can write the following chain
$$0.30538\sim \frac{1}{e}-\frac{1}{16}=\sum_{n\space\in\space S^*}\frac{1}{n}=\sum_{n\space\in\space S^*}\frac{\log n}{n\log n}\lt\sum_{n\space\in\space S^*}\frac{\log n}{n(\log n - 1)}=\sum_{n\space\in\space S^*}\frac{1}{n - \frac{n}{\log n}}\lt\sum_{n\space\in\space S^*}\frac{1}{n - \pi(n)}\lt\sum_{n\space\in\space S^*}\frac{1}{n - \frac{1.25506\space n}{\log n}}=\sum_{n\space\in\space S^*}\frac{\log n}{n(\log n - 1.25506)}=\sum_{n\space\in\space S^*}\frac{\log n - 1.25506}{n(\log n - 1.25506)}+1.25506\cdot\sum_{n\space\in\space S^*}\frac{1}{n(\log n - 1.25506)}=\sum_{n\space\in\space S^*}\frac{1}{n}+1.25506\cdot\sum_{n\space\in\space S^*}\frac{1}{n(\log n - 1.25506)}=\frac{1}{e}-\frac{1}{16}+1.25506\cdot\sum_{n\space\in\space S^*}\frac{1}{n(\log n - 1.25506)}\lt\frac{1}{e}-\frac{1}{16}+\frac{1.25506}{2}\cdot\sum_{n\space\in\space S^*}\frac{1}{n}=\Big(\frac{1}{e}-\frac{1}{16}\Big)\Big(1+\frac{1.25506}{2}\Big)\sim 0.49701$$
In other words, if
$$\sum_{n\space\in\space S^*}\frac{1}{n}=\frac{1}{e}-\frac{1}{16}$$
then also the series
$$\sum_{n\space\in\space S^*}\frac{1}{n - \pi(n)}$$
converges and, furthermore,
$$0.30537\lt\sum_{n\space\in\space S^*}\frac{1}{n - \pi(n)}\lt0.49702$$
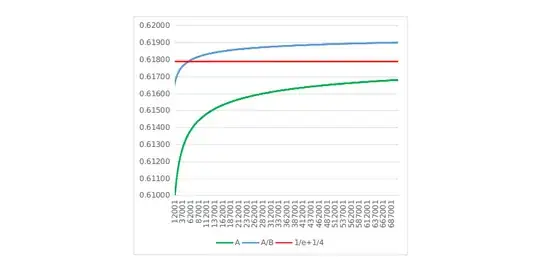
As can be seen, the conjectured convergence value of the series
$$\sum_{n\space\in\space S^*}\frac{1}{n - \pi(n)}=1-\frac{1}{2}-\frac{1}{10}=0,4$$
falls close to half in the upper range.