4

I am trying to work on an exercise which claims that

If two representations ρ and σ, on Hilbert spaces H and G respectively, are each unitarily equivalent to a subrepresentation of the other, then they are unitarily equivalent, which is called the Schroeder-Bernstein theorem for representations of C*-algebras.

You can refer to https://en.wikipedia.org/wiki/Schr%C3%B6der%E2%80%93Bernstein_theorems_for_operator_algebras for more details about the theorem and an outline of the proof.

I am now confused about the outline he gives in the wiki, where he claims that by induction we can get $\rho_1\simeq (\bigoplus_{i\geq1}\rho_i^\prime)\bigoplus (\bigoplus_{i\geq1}\sigma_i^\prime)$. I am not sure we can get this by induction. What we do get is that $\rho_1\simeq (\bigoplus_{i=1}^{n}\rho_i^\prime)\bigoplus 1(\bigoplus_{i=1}^{n}\sigma_i^\prime)\bigoplus \rho_{n+1}$ for every $n\in\mathbb{N}$, where $\rho_1\simeq \rho_{n+1}$, but this doen't mean that we can claim the equation for countable infinity.

Any help will be truly grateful!

Yanyu
  • 430

1 Answers1

3

The section "Representations of C$^*$-algebras" is poorly written, but the idea of what needs to be done is in the previous section.

To work as in the subspace case, we first note that a required hypothesis is that both representations are non-degenerate (otherwise, the result is not true, as we can consider cases like $\rho$ and $\sigma=\rho\oplus0$ and there is no unitary between the ambient Hilbert spaces). It follows that $\dim H=\dim G$, and so we may assume without loss of generality (at the cost of one more unitary conjugation) that $G=H$.

By hypothesis $\rho=\sigma_1\oplus\rho_1'$, with $\sigma_1\simeq\sigma$. This means that there exists a subspace $N_1$ with $\rho|_{N_1}=\sigma_1$. Let $R_1=H\ominus N_1$, so $\rho|_{R_1}=\rho_1'$. Next we have $\sigma_1=\rho_2\oplus\sigma_2'$, where $\rho_2\simeq\rho$. So there exists a subspace $M_1\subset N_1$ with $\sigma_1|_{M_1}=\rho_2$. Let $S_1=N_1\ominus M_1$, so that $\sigma_1|_{S_1}=\sigma_2'$. By induction we get subspaces and representations $$ \rho_k=\sigma_k\oplus\rho_k',\qquad \sigma_k=\rho_{k+1}\oplus\sigma_{k+1}', $$ $$ \rho_k|_{N_k}=\sigma_k,\quad \rho_k|_{R_k}=\rho_k', $$ $$ \sigma_k|_{M_k}=\rho_k,\quad \sigma_k|_{S_k}=\sigma_{k+1}', $$ $$ R_j=M_{j-1}\ominus N_j,\qquad S_j=N_j\ominus M_j $$ and $$ H\supset N_1\supset M_1\supset N_2\supset M_2\supset\cdots $$ Since each inclusion $N_{j+1}\subset M_j$ and $M_j\subset N_j$ arises from the same decomposition, we have $\rho_j'\simeq\rho_k'$, $\sigma_j'\simeq\sigma_k'$ for all $k,j$. Here's a poor man's picture of the inclusions.

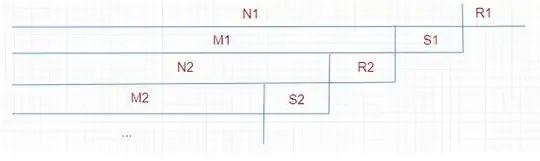
enter image description here

If we let $Q=\bigcap_jM_j=\bigcap_jN_j$, we can write

$$ H=Q\oplus\,\bigoplus_{k=1}^\infty R_k\,\oplus\,\bigoplus_{k=1}^\infty S_k,\qquad N_1=Q\oplus\,\bigoplus_{k=2}^\infty R_k\,\oplus\,\bigoplus_{k=1}^\infty S_k. $$ We have $$ \rho|_{R_k}=\rho_k',\qquad \rho|_{S_k}=\sigma_{k+1}',\qquad \sigma_1|_{R_{k+1}}=\rho_{k+1}',\qquad \sigma_1|_{S_k}=\sigma_{k+1}', $$ and, very importantly, $\rho|_Q=\sigma_1|_Q$. Let $\gamma=\rho|_Q=\sigma|_Q$. The decomposition then gives us $$ \rho=\gamma\oplus\,\bigoplus_{k=1}^\infty \rho_k'\,\oplus\,\bigoplus_{k=1}^\infty \sigma_{k+1}',\qquad \sigma_1=\gamma\oplus\,\bigoplus_{k=2}^\infty \rho_k'\,\oplus\,\bigoplus_{k=1}^\infty \sigma_{k+1}'. $$ Now one can generate a unitary by shifting the index in the sum of the $\rho'$ to get $\rho\simeq \sigma_1$.

Martin Argerami
  • 217,281
  • Thanks for the answer, you are right, there should always be a copy of $\rho$ on the right, I have edited the question to fix the typo. – Yanyu Mar 25 '22 at 06:58
  • I am trying to do read the proof again, but I get confused about the claim that $\rho_j^\prime\cong \rho_k^\prime$. How to get this claim precisely? The problem here is that if we denote the partial isometry by $U$, which is the partial isometry coming from the equivalence by $\rho_1 \cong \rho_2 $. Similarly, we can get a partial isometry from the equivalence by $\sigma_1 \cong \sigma_2 $. However, in general, we may not be able to say that $U=V\oplus W$ for some operator $W$, so it may not be easy to verify the claim. Any suggestions? – Yanyu Jun 12 '22 at 16:34
  • You have that $\rho_{k+1}$ is unitarliy equivalent to $\rho_k$. The decompositions $\rho_k=\sigma_k\oplus\rho_k'$ and $\rho_{k+1}=\sigma_{k+1}\oplus\rho_{k+1}'$ are each obtained from $\rho=\sigma_1\oplus\rho_1'$ via the respective isometry that does $\rho_k\simeq \rho$ and $\rho_{k+1}\simeq \rho$. So $\rho_k\simeq\rho_{k+1}$ via the unitary that does $R_k\to R_1\to R_{k+1}$. – Martin Argerami Jun 13 '22 at 03:12
  • Yes, that's right, we know that $\rho_k\cong \rho_{k+1}$ easily, but I think what we really need here is that $\rho_k^\prime\cong \rho_{k+1}^\prime$? It is not simple. I have described my thought In a new question, which is linked here: https://math.stackexchange.com/questions/4471391/a-question-about-the-proof-of-schr%c3%b6der-bernstein-theorems-for-c-algebras?noredirect=1&lq=1 Thanks a lot for your help! – Yanyu Jun 13 '22 at 03:18
  • I missed the primes in the last line of my comment. But as I already said in the comment and also in my answer, $\rho_k'$ and $\rho_{k+1}'$ come from the same decomposition, just applied to different copies of $\rho$ (namely, $\rho_k$ and $\rho_{k+1}$). So couldn't possibly not be unitarily equivalent. – Martin Argerami Jun 13 '22 at 03:22
  • When we say they come from the same decomposition, I think we don't consider the unitary we used. The problem here is the unitarily equivalent we used may not be the same. – Yanyu Jun 13 '22 at 03:42
  • To be more specific, For example, if we know that $\rho\cong \pi$, $\rho =\rho_1\oplus \rho_2$, $\pi\cong \pi_1\oplus \pi_2$, $\rho\cong \pi$ and $\rho_1\cong \pi_2$, do we know that $\rho_2\cong \pi_2$? I think this is how we get the claim that $\rho_k^\prime\cong \rho_j^\prime$. At first, I think it should be easy, but when I try to write it, I find it is not as simple as it seems. We know that $U\rho(a)U^=\pi(a)$, and $V\rho_1(a)V^=\pi_1(a)$. However, it is hard to say that $U=diag{V,W}$ (At least not immediately), so we may not know that $\rho_2\cong \pi_2$. – Yanyu Jun 13 '22 at 03:43
  • You seem to be thinking it is some kind of cancellation; it is not. It is the same decomposition, moved to another part of the space by a unitary. – Martin Argerami Jun 13 '22 at 03:57
  • I think they are the same decomposition in the unitarily equivalent sense, we just know that $\rho\cong \rho_k \cong \rho_{k+1}$ instead of $\rho=\rho_k=\rho_{k+1}$. However, the example above shows that the unitary operator here should be kind of crucial such that we can't ignore it. – Yanyu Jun 13 '22 at 04:05
  • Let us continue this discussion in chat. – Yanyu Jun 13 '22 at 04:11