Can't find w graphing function local maximum/minimums using derivative for equation $y = (a + bx)\cos(x)$ to the desired level of precision

Question

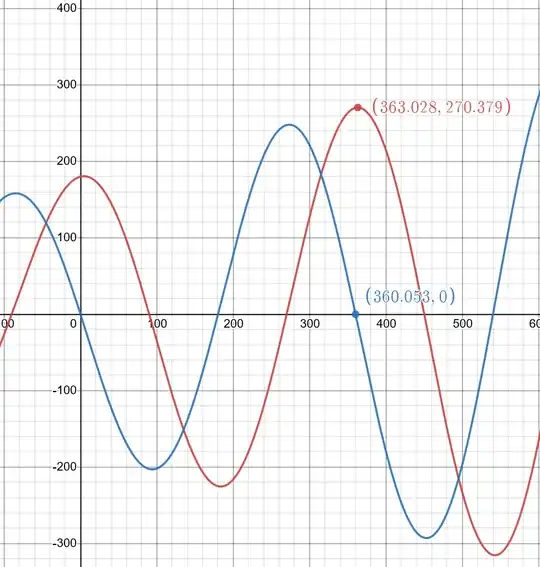
I want to calculate local maximums and minimums for: $$y = (a + bx) \cos{x}$$

The derivative is: $$\dfrac{dy}{dx} = b \cos{x} - (a+bx)\sin{x}$$

I then tried to graph these functions to find where $\dfrac{dy}{dx}=0$, but the points where the derivative is equal to zero don't exactly coincide with the local maximums of the original function.

For this example, the constants are $a=180$ and $b=0.25$.

The red line is the function and the blue is the derivative. As you can see, the derivative equals zero when $x=360.053$, but the function is not at its maximum on that point. It reaches the maximum at $x=363.028$.

Can someone tell me what's happening? I think the slope should be zero exactly where the maximum is. Did I do anything wrong?

Answer 1

Your function has a factor with period $2\pi$, and your plot has a period a little below $400$. So I guess your angles are in degrees.

But then your derivative is wrong: $\cos'=-\sin$ is only true for angles in radians.

Therefore, the roots of the derivative are not where the blue curve crosses the $x$ axis.

See Derivative of the sine function when the argument is measured in degrees

Here, with $x$ in degrees but with cosine being the usual one (i.e. with argument in radians, so that we can differentiate), we have

$$f(x)=(180+\frac x4)\cos(\frac{\pi}{180}x)$$

$$f'(x)=\frac x4\cos(\frac{\pi}{180}x)-\frac{\pi}{180}(180+\frac x4)\sin(\frac{\pi}{180}x)$$

To be able to see something on the following plot, $f$ (red) and $30f'$ (blue) are shown.