There are a few different questions here. I'll try to address them from one angle, but feel free to clarify that you were looking for something else.
What is the interpretation of the value computed if the integrand is a non-constant function?
There are many interpretations of a double integral. A big list is covered in this answer to "Visualization of double integrals". One of the more popular interpretations is as the signed volume (negative if $f(x,y)$ is negative) under the surface $z=f(x,y)$ above the region of integration.
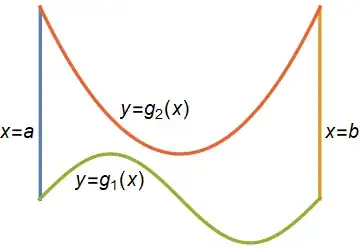
For example, if we have that $D$ is the region bounded by $x=a:=0$, $x=b:=2\pi$, $y=g_1(x):=\sin(x)$, and $y=g_2(x):=(x-\pi)^2/3+1$, then $D$ is the region inside those four curves:
Then, if $f(x,y)=\left((x-\pi)^2+(y-1)^2\right)/4+2$, a plot of $f(x,y)$ over $D$ would look like:

and the double-integral $\iint_D f(x,y)\,\mathrm dA$ would calculate the bounded volume, which looks like this:
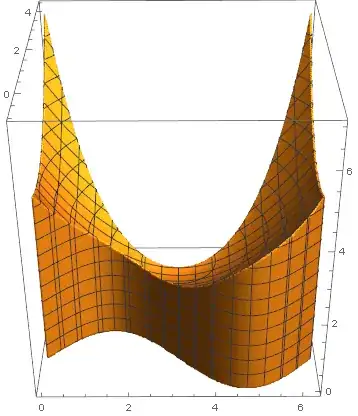
This volume could be calculated as an iterated integral like $$\int_a^b\int_{g_1(x)}^{g_2(x)}f(x,y)\,\mathrm dy\,\mathrm dx=\int_0^{2\pi}\int_{\sin(x)}^{(x-\pi)^2/3+1}\left(\dfrac{(x-\pi)^2+(y-1)^2}{4}+2\right)\,\mathrm dy\,\mathrm dx$$
what can we visualise the first integral with respect to y as, as in what would this area look like before we compute the second integral?
For each value of $x$, $\int_{g_1(x)}^{g_2(x)}f(x,y)\,\mathrm dy$ has particular numbers for the upper and lower bounds of integration, and $f(x,y)$ reduces to a function of a single value of $y$. For example, at $x=c:=3\pi/2$, the above functions would have $$\int_{g_1(c)}^{g_2(c)}f(c,y)\,\mathrm dy=\int_{\sin(3\pi/2)}^{(3\pi/2-\pi)^2/3+1}\left(\dfrac{(3\pi/2-\pi)^2+(y-1)^2}{4}+2\right)\,\mathrm dy$$
We can visualize this as the area of the $x=c$ slice of the volume discussed above:
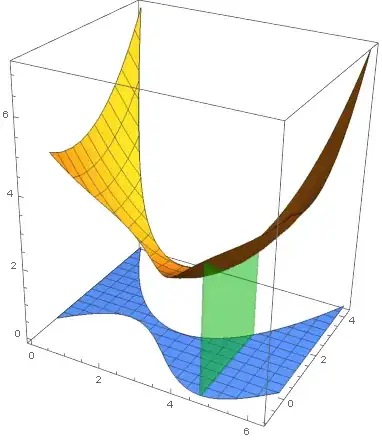
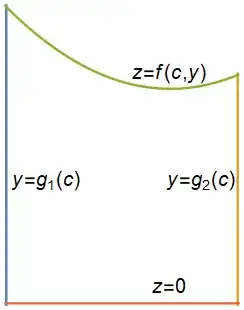
This shape whose area is calculated with the above integral lies in a plane parallel to the $yz$-plane, and is bounded by the curves $y=g_1(c)=\sin(3\pi/2)=-1$, $y=g_2(c)=(3\pi/2-\pi)^2/3+1=\pi^2/12+1$, $z=0$, and $z=f(c,y)=\left(\dfrac{(3\pi/2-\pi)^2+(y-1)^2}{4}+2\right)=\dfrac{(y-1)^2+\pi^2/4}{4}+2$, as shown here:
I have found that most of what I have seen relating to my above questions is that they are talking about the xyz plane where I just want to understand the xy plane for now.
The most common interpretations of a single integral are of an area in the 2D plane. So when moving up to a double integral, it's common to use one more dimension, as in the 3D images above. If you really prefer to think of the double integral as calculating something intrinsic to 2D (as in the case of area when $f(x,y)=1$), then you can use another interpretation that would live in 1D in the case of a single integral.
One choice is that of charge and charge density, as mentioned in the answer to "Visualization of double integrals" I'd linked. Then a single integral could be adding up linear charge density to get a total charge. A double integral could be adding up planar/areal/surface charge density to get a total charge. And the single integral $\int_{g_1(c)}^{g_2(c)}f(c,y)\,\mathrm dy$ could add up bits of surface charge density times the length $\mathrm dy$ to get a horizontal linear charge density that could then be multiplied by bits of length $\mathrm dx$ and added up to get the total charge.
We could draw a 2D picture using color and/or brightness to indicate densities, but I don't think it's easy to think of summed color/brightness equalling another color/brightness (that could then be summed again), so I personally prefer thinking about the 3D pictures and their 2D slices whenever possible.




