0

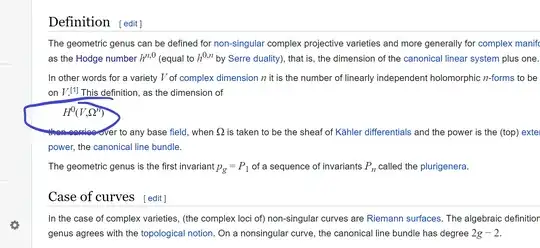
Here is the page I was reading.. I tried reading more into what Hodge numbers are and it was too complex for the short amount of time I had but I figured the $0$ probably indicated something like a "(p,q)-forms" where $p=n$ and $q=0$; because it is just for non-singular complexes from what I'm reading & because I haven't studied that type of form yet from what I recall.

Is it actually topological notation for $0^{th}$ cohomology group of $(V,\Omega^{n})$ though because I haven't done the type of calculation for dimensions of cohomology groups before just introductory type of dimension such as $0$-dimension is for points and $1$-dimensional is for lines & etcetera. Maybe the dimension is a type of dimension of something like $\mathbb{Z} \oplus \mathbb{Z}=H^{0}(X)$ but the part about forms is difficult to start out with and I haven't done a lot of "topology" aside from Hatcher's Algebraic Topology and learning about Zariski topology and I even stopped altogether when I tried to read about Riemann-Roch theorem before.

Figure 1

rawiga golf club skateboarder
  • 174
  • I'm not sure what link exactly you're seeing between $H^0(V,\Omega^n)$ and $H^n(V,\Omega^n)$ based on those figures. Could you elaborate on what exactly the interpretation issue is? – Thorgott Feb 28 '22 at 20:06
  • "If they were 'equal' that makes $H^0(V, \Omega^n)$ into $H^n(V, \Omega^n)$" I don't understand where this is coming from. Note, the latter is always one-dimensional ($h^{n,n}(V) = 1$). – Michael Albanese Feb 28 '22 at 22:06
  • 1
    I thought $H^{0}(V,\Omega^{n})$ was a Hodge number & now I think it could be a cohomological notation instead... – rawiga golf club skateboarder Mar 01 '22 at 05:27
  • 2
    $H^0(V,\Omega^n)$ is the $0$-th cohomology group of the sheaf $\Omega^n$ of holomorphic $n$-forms on $V$. The $0$-th cohomology group of a sheaf is naturally isomorphic to its group of global sections, which are in this case by definition the holomorphic $n$-forms on $V$. – Thorgott Mar 01 '22 at 12:33

0 Answers0