1

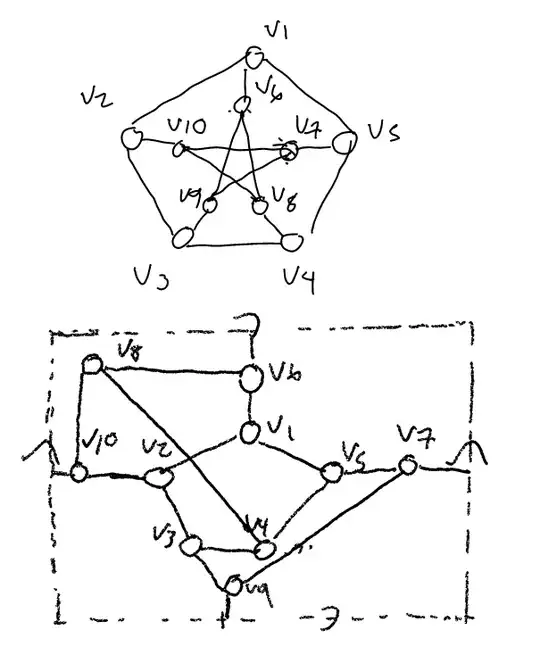
In relation to the question asked here Genus of Petersen graph could a possible solution be to construct a rectangle which represents an embedding on a torus where the opposite edges are identified (essentially like a rectangle space in a video game where if you continue down you end up coming down the top of the rectangle and if you go right in the rectangle you end up entering from the left side of the rectangle and vice versa )? We thus show that the Petersen graph can be embedded in this rectangle where there is only one crossing s.t the genus is equal to 1.

I have attached a picture as a possible solution where we get exactly one crossing. Torus representation of a Petersen graph

PianoMath
  • 87
  • Wouldn't this drawing imply that the genus of the Petersen graph is two? – AKemats Feb 25 '22 at 13:48
  • 1
    You want to embed the Petersen graph either in the plane with only one crossing (which is unfortunately impossible) or in the torus with $0$ crossings (see this). An embedding in the torus with a crossing tells us that there is an embedding in the double torus with no crossings, which only tells us that the genus is at most two. – Misha Lavrov Feb 25 '22 at 14:19

0 Answers0