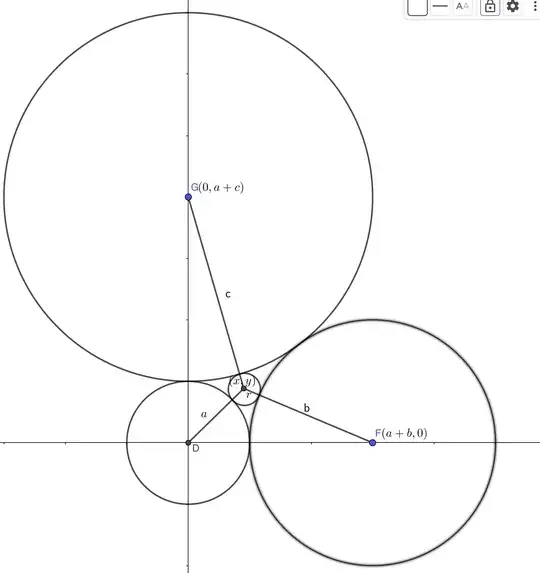
Since their centres form a right-angled triangle, we can arrange the four circles as shown below:
Although there are ready-made formula in this site and in the history such as Descartes four circle theorem, stating that
$$\left( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \frac{1}{R_4} \right)^2
=
2 \left( \frac{1}{R_1^2} + \frac{1}{R_2^2} + \frac{1}{R_3^2} + \frac{1}{R_4^2} \right),
$$
I want to find a new one by elementary method myself.
Using the fact that when two circles touch each other, the distance between their centre is exactly the sum of their radii, we get 3 equations
$$ \begin{array}{l} x^{2}+y^{2}=(a+r)^{2} \qquad\qquad \,\cdots(1) \\ [x-(b+a)]^{2}+y^{2}=(b+r)^{2} \cdots(2)\\ x^{2}+[y-(c+a)]^{2}=(c+r)^{2} \cdots(3) \end{array} $$ where $(x,y)$ is the centre of the inscribed circle.
(1)-(2) yields $$ x^{2}-[x-(b+a)]^{2}=(a+r)^{2}-(b+r)^{2} $$
$$ x=a+\frac{a-b}{a+b} r \tag*{(4)} $$
(1)-(3) yields $$ y^{2}-[y-(c+a)]^{2}=(a+r)^{2}-(c+r)^{2} $$
$$ y=a+\frac{a-c}{a+c}r \tag*{(5)} $$ Putting them into (1) yields $$ \left(a+\frac{a-c}{a+c} r\right)^{2}+\left(a+\frac{a-b}{a+b} r\right)^{2}=(a+r)^{2} $$ Then the radius $r$ is given as the positive root of the quadratic equation
$$ \left[\left(\frac{a-c}{a+c}\right)^{2}+\left(\frac{a-b}{a+b}\right)^{2}-1\right] r^{2}+2 a\left(\frac{a-c}{a+c}+\frac{a-b}{a+b}-1\right)r+a^{2}=0 $$
By the way, we can find the coordinates of the centre by putting $r$ back to (4) and (5).
Example 1
If the radii of three given circle are $1, 2$ and $3$, then the quadratic equation becomes $$ -\frac{23}{36} r^{2}-\frac{11}{3} r+1=0 \\ 23 r^{2}+132 r-36=0\\ r=\frac{6}{23}, $$ and its centre is $\left(\dfrac{21}{23}, \dfrac{20}{23}\right).$
Example 2
If the radii of three given circle are $2, 3$ and $10$, then the quadratic equation becomes
$$\left(\frac{1}{25}+\frac{4}{9}-1\right) r^{2}+4\left(-\frac{1}{5}-\frac{8}{12}-1\right) r+4=0$$$$ r=\frac{15}{29} $$ and its centre is $\left(\dfrac{55}{29}, \dfrac{48}{29}\right)$.
My Question
Is there any other method? Your comments and alternative method are highly appreciated.
