I refer to a previous post of mine in which it is defined the recurrence relation (now OEIS sequences A349576 and A349982) $$ x_{n+1} = \frac{x_{n} + x_{n-1}}{(x_{n},x_{n-1})} + c\;\;\;\;\;\;\;(1)$$ where $(x_{n},x_{n-1})$ is the gcd of $x_{n}$ and $x_{n-1}$.
This recurrence relation often generates periodic sequences with periods depending on the value of the integer constant $c$.
I wondered what dynamics I would have obtained by eliminating the dependence on such constant. One of the most interesting behaviors is shown by the following relation $$ x_{n+1} = \frac{x_{n} + x_{n-1}}{(x_{n},x_{n-1})} + (x_{n},x_{n-1})\;\;\;\;\;\;\;(2)$$ One might expect that the character (periodic or non-periodic) of the sequences generated by relation (2) depends on the choice of the initial conditions $x_0$ and $x_1$. But things are a little different.
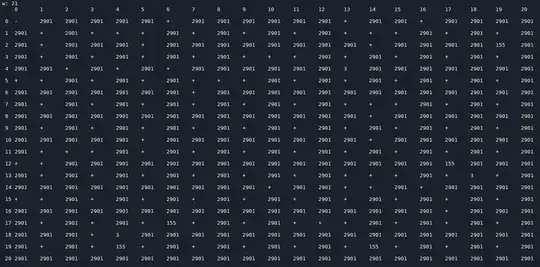
I made some numerical experiments. The following screenshot shows the results obtained.
The image consists of a $21$ x $21$ matrix $T$ in which:
- $x_0$ is the row index;
- $x_1$ is the column index;
- $t_{\,x_0,\,x_1}$ represents the period of the sequence generated by the recurrence relation $(2)$ starting with the initial conditions $x_0,\,x_1$ (the symbol "+" stands for a probably non-periodic sequence).
Up to $21$ x $21$ only $3$ possible periods appear:
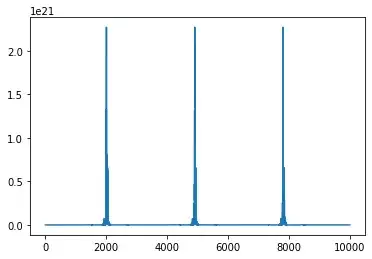
- $2901$, $\,x_n=x_{n+2901}\,$ for $\,n \ge 278$, with a peak value of $2269429312765395470820$ $(\sim 2.27\cdot 10^{21})$
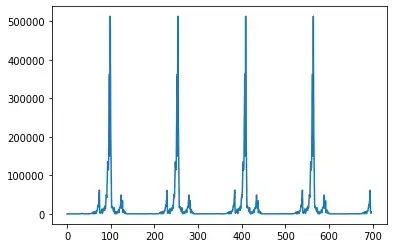
- $155$, with a peak value of $513582$ (e.g. $x_0=2,x_1=19$)
- $3$, with a peak value of $60$ (e.g. the pair $x_0=13,x_1=18$ generates the sequence $13,18,32,27,60,32,27,60,32,...$).
Will different values appear for the period by extending the search scope?
And why do the three indicated values ($2901, 155, 3$) appear and not others?
Edit
Other three period lengths have been found:
- $9\,$ (see Peter's comment);
- $53\,$ ($x_0=70,x_1=207$);
- $84\,$ ($x_0=38,x_1=200$).