$Spin(6,2) = SU(2, 2, \mathbb{H})$

Question

On Wikipedia https://en.wikipedia.org/wiki/Spin_group#Indefinite_signature, it says $Spin(6,2) = SU(2, 2, \mathbb{H})$. But I cannot find any reference. Does anyone know one, or any other references which explains what this spin group is? Thank you in advance!

Answer 1

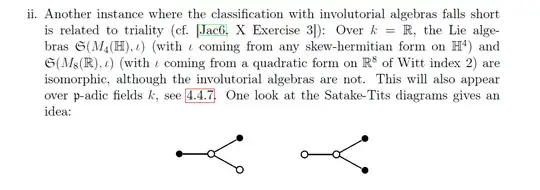
This is a case that shows what a great thing the Tits index a.k.a. Satake diagram is. Here is Remark 4.5.20.ii from my thesis:

(The reference Jac6 is Lie Algebras by Nathan Jacobson. Interscience Tracts in Pure and Applied Mathematics, Number 10. John Wiley and Son, Inc. New York, 1962.)

The algebra belonging to the thing on the right would almost always be written $\mathfrak{so}(6,2)$, and then of course its corresponding simply connected group is $Spin(6,2)$. The thing on the left, unfortunately, seems to not have a standard name (neither the Lie algebra nor its corresponding simply connected group), so in every source we have to check the nomenclature. In Schulte-Hengesbach's diploma thesis mentioned by Dietrich Burde in a comment, the Lie algebra is called $\mathfrak{sp}(2, \mathbb H)$; in Onishchik/Vinberg's tables, the Lie algebra is called $\mathfrak{u}^*_{4}(\mathbb H)$; apparently your source calls the corresponding simply connected group $SU(2,2, \mathbb H)$.

Finally, here is how Tits describes both forms in his article in the Boulder Proceedings (p.56/57). He talks about groups. The form on the left is, in Tits' notation, $^1D^{(2)}_{4,2}$ (i.e. $n=4, d=2, r=2$), and he would call it $SU_4(\mathbb H, h)$ for a certain $h$ as described below (I think Jacobson's and my description above matches rather his "equivalent description for $d \ge 2$", but I'm not entirely sure about that). The form on the right is $^1D^{(1)}_{4,2}$ (i.e. $n=4, d=1, r=2$).

Answer 2

1. On one hand, the Lie group $SO^+(6,2;\mathbb{R})$ has 16 compact and 12 non-compact dimensions, in total 28 real dimensions.

   On the other hand, the most natural definition of $SU(2,2;\mathbb{H})$ would be the set of $4\times 4$ quaternionic matrices that are unitary wrt. a split metric of signature (2,2), and has unit determinant. However this Lie group has 20 compact and 16 non-compact dimensions, in total 36 real dimensions, cf. my Math.SE answer here. So Wikipedia [August 2023] must either be wrong or use another definition. Here we will instead consider the Lie group $U^{\ast}(4,\mathbb{H})$ to be defined in eq. (1) below.

2. Let us define the Lie group [1] that is invariant wrt. an anti-Hermitian metric $$\begin{align} U^{\ast}(n,\mathbb{H})~:=~&\{x\in{\rm Mat}_{n\times n}(\mathbb{H})\mid x^{\dagger}(j{\bf 1}_{n\times n})x=j{\bf 1}_{n\times n}\}\cr ~\cong~&\{M\in{\rm Mat}_{2n\times 2n}(\mathbb{C})\mid M^{\dagger}\Omega M=\Omega,~\overline{M}\Omega=\Omega M\}, \cr ~\cong~&\{M\in{\rm Mat}_{2n\times 2n}(\mathbb{C})\mid M^tM={\bf 1}_{2n\times 2n},~\overline{M}\Omega=\Omega M\}, \cr \Omega ~:=~&{\bf 1}_{n \times n}\otimes \omega~=~-\Omega^t, \cr \omega ~:=~&\mathrm{i}\sigma_2~=~-\omega^t , \cr \Omega^2~=~&-{\bf 1}_{2n \times 2n},\end{align}\tag{1}$$ cf. my Math.SE answer here.

3. The condition $$\overline{M}\Omega ~=~ \Omega M \tag{2} $$ is the condition $$ \overline{m}_{ij}\omega ~=~\omega m_{ij}, \qquad i,j~\in~\{1,\ldots,n\},\tag{3} $$ that each of the $2\times 2$ blocks $m_{ij}$ in $$M~=~\begin{pmatrix} m_{11} &\ldots & m_{1n} \cr \vdots &\ddots & \vdots \cr m_{n1} &\ldots & m_{nn}\end{pmatrix}~\in~{\rm Mat}_{2n\times 2n}(\mathbb{C})\tag{4}$$ can be identified with a quaternion, cf. e.g. my Phys.SE answer here.

4. Proposition: $\det(M)=1$ for a matrix $M$ in eq. (1). Proof: To be filled later. $\Box$ Corollary: $$ SU^{\ast}(n,\mathbb{H})~=~U^{\ast}(n,\mathbb{H}), \tag{5}$$ where $S$=special=unit determinant.

5. It follows that the complexification is the complex special orthogonal group $$ U^{\ast}(n,\mathbb{H})_{\mathbb{C}}~\cong~\{M\in{\rm Mat}_{2n\times 2n}(\mathbb{C})\mid M^tM={\bf 1}_{2n\times 2n},~\det(M)=1\}~=~SO(2n,\mathbb{C}).\tag{6}$$

6. By choosing elements of the form $x\in{\rm Mat}_{n\times n}(\mathbb{R}\oplus j\mathbb{R})$ in eq. (1), we see that that $$U(n)~\subseteq~ U^{\ast}(n,\mathbb{H}) \tag{7} $$ is a compact subgroup of $U^{\ast}(n,\mathbb{H})$. In fact we shall see below that $U(n)$ is a maximal compact subgroup of $U^{\ast}(n,\mathbb{H})$.

7. The corresponding Lie algebra is $$\begin{align}u^{\ast}(n,\mathbb{H}) ~=~&\{x\in{\rm Mat}_{n\times n}(\mathbb{H})\mid x^{\dagger}=jxj\} \cr ~=~&\{x\in{\rm Mat}_{n\times n}(\mathbb{H})\mid (jx)^{\dagger}=jx\}\cr ~\cong~&\{m\in{\rm Mat}_{2n\times 2n}(\mathbb{C})\mid m^t =-m,~m^{\dagger}=\Omega m\Omega\}\cr ~=~&\left\{\left. m=\begin{pmatrix} a & b \cr c & d \end{pmatrix}\in {\rm Mat}_{2n\times 2n}(\mathbb{C}) \right| a^t=-a, b^{\dagger}=b, c= -b^t, d=-a^{\dagger} \right\}. \end{align}\tag{8} $$ It has $\frac{n(n-1)}{2}+\frac{n(n+1)}{2}=n^2$ [real antisymmetric = anti-Hermitian] compact and $\frac{n(n-1)}{2}+\frac{n(n-1)}{2}=n(n-1)$ [imaginary antisymmetric = Hermitian] non-compact generators, respectively. In total, $$ \dim_{\mathbb{R}}u^{\ast}(n,\mathbb{H})~=~n(2n\!-\!1).\tag{9}$$

8. Central question:

   Could $$u^{\ast}(n,\mathbb{H})~\stackrel{?}{\cong}~so(p,q;\mathbb{R})\tag{10}$$ be isomorphic to an indefinite orthogonal Lie algebra?

   Well, $so(p,q;\mathbb{R})$ has $\frac{p(p-1)}{2}+\frac{q(q-1)}{2}$ [real antisymmetric = anti-Hermitian] compact and $pq$ [real symmetric = Hermitian] non-compact generators, respectively. In total $$ \dim_{\mathbb{R}}so(p,q;\mathbb{R})~=~\frac{(p+q)(p+q-1)}{2}.\tag{11}$$ Comparing eqs. (9) & (11) yields $2n=p+q$. Together with $pq=n(n-1)$ this leads to $$ \left. \begin{array}{lcr} p&=& n\pm r \cr q&=& n\mp r \end{array}\right\} \quad\text{where} \quad r~:=~\sqrt{n}~\in~\mathbb{N}_0. \tag{12} $$ In other words, $n=r^2$ should be a square.

   Could the compact subalgebras $$u(n)~\cong~ su(n)\oplus u(1) ~\stackrel{?}{\cong}~so(p,\mathbb{R})\oplus so(q,\mathbb{R})\tag{13}$$ be isomorphic?

   Well, then clearly $p\leq 2 \vee q\leq 2 $. Comparing with eq. (11) we see that $n\leq 4$. It follows that there are at most 2 examples: $$(n,p,q)~=~(1,2,0) \qquad\text{and} \qquad(n,p,q)~=~(4,6,2)\tag{14}$$ up to a trivial $p\leftrightarrow q$ symmetry.

9. First example: $$\begin{align}U^{\ast}(1,\mathbb{H}) ~\cong~&\left\{\left. M=\begin{pmatrix} \alpha & \beta \cr -\bar{\beta} & \bar{\alpha} \end{pmatrix}\in {\rm Mat}_{2\times 2}(\mathbb{C}) \right| M^t=M^{-1}\right\}\cr ~=~&\left\{\left. M=\begin{pmatrix} \alpha & \beta \cr -\bar{\beta} & \bar{\alpha} \end{pmatrix}\in {\rm Mat}_{2\times 2}(\mathbb{R}) \right| |\alpha|^2+|\beta|^2=1\right\}\cr ~=~&SO(2,\mathbb{R}). \end{align}\tag{15} $$

10. Second and main example: $$U^{\ast}(4,\mathbb{H})~\cong~Spin^+(6,2;\mathbb{R})/\mathbb{Z}_2~\cong~SO^+(6,2;\mathbb{R}).\tag{16}$$ Both Lie groups have 16 compact and 12 non-compact dimensions, in total 28 real dimensions. The compact subgroups are locally isomorphic $$ U(4)~\cong~[SU(4)\times U(1)]/\mathbb{Z}_4 ~\cong~ [Spin(6,\mathbb{R})\times SO(2,\mathbb{R})]/\mathbb{Z}_4, \tag{17}$$ cf. e.g. this Math.SE post and this Phys.SE post. The corresponding Lie algebras satisfy $$\begin{align} u^{\ast}(4,\mathbb{H})~\cong~&u(4)\oplus \mathfrak{p}~\cong~so(6,2;\mathbb{R}),\cr so(4,\mathbb{R})\oplus j~{\rm Sym}^2(\underline{\bf 4}) ~\cong~&u(4)~\cong~su(4)\oplus j~u(1) ~\cong~so(6,\mathbb{R})\oplus j~so(2,\mathbb{R}),\cr \mathfrak{p}~\cong~&i~so(4,\mathbb{R})\oplus k~so(4,\mathbb{R}) ~\cong~\underline{\bf 6}\otimes \underline{\bf 2},\cr \mathbb{Z}_4~\cong~&\{\pm 1,\pm j\},\cr so(4,\mathbb{R})~\cong~&\bigwedge\!{}^2 \underline{\bf 4}~\cong~\underline{\bf 6}, \qquad so(6,\mathbb{R})~\cong~\bigwedge\!{}^2 so(4,\mathbb{R}), \cr [u(4),\mathfrak{p}]~\subseteq~&\mathfrak{p},\qquad [\mathfrak{p},\mathfrak{p}]~\subseteq~u(4),\cr [so(4,\mathbb{R}),{\rm Sym}^2(\underline{\bf 4})]~\subseteq~&{\rm Sym}^2(\underline{\bf 4}),\qquad \{so(4,\mathbb{R}),{\rm Sym}^2(\underline{\bf 4})\}_+~\subseteq~{\rm Sym}^2(\underline{\bf 4}),\cr [{\rm Sym}^2(\underline{\bf 4}),{\rm Sym}^2(\underline{\bf 4})]~\subseteq~&so(4,\mathbb{R}),\qquad \{so(4,\mathbb{R}),so(4,\mathbb{R})\}_+~\subseteq~{\rm Sym}^2(\underline{\bf 4}). \end{align} \tag{18} $$

References:

1. W. Fulton & J. Harris, Representation theory, 1991; p. 433.