1

So a problem I've been struggling with for a while is the following

Assume you are placed within the unit circle at a unspecified location $P$, and a predator is placed somewhere on on the circumference of the circle. As your velocity on land is far greater than the predator, you escape if you manage to reach the shore first. However, while in water the predators velocity is 4 times greater than yours. What is the probability you are able to escape, assuming you are just as likely to be at any point within the circle.

Naive attempt

So, I simplified the problem due to rotation symmetry and drew the following

enter image description here

With $L$ being the location of the predator and $G$ being our random position. Switching to polar coordinates gives

$$\color{blue}{\text{Arc = }} \pi - 2 \theta, \qquad \color{red}{\|GE\| = } 2 \cos \theta - \rho$$

Since the red segment must be 4 times greater than the blue arc we obtain

$$ \rho > 2 \cos \theta - \frac{\pi - 2\theta}{4}$$

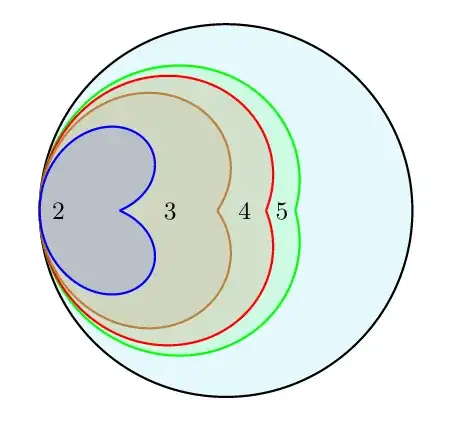
In order to escape. For different velocities it can look like this

enter image description here

Where you are captured no matter what if you are within the colored circle. Finding the probability of not getting captured is now simply

$$P = 1 - \frac{1}{\pi/2} \int_0^{\pi/2} \frac{1}{2}\bigl(2 \cos \theta - \frac{\pi - 2\theta}{4}\bigr)^2\,\mathrm{d}\theta = \frac{2}{\pi} - \frac{\pi^2}{96} \approx 53\%$$

Issue

My solution assumes that we run in the diametrically opposite direction.

However, looking at the following picture it is not clear this is optimal

enter image description here

Maybe following the normal ($m$) gives a better result, than diametrically opposite ($i$), or perhaps the optimal path is somewhere between ($2$).

Questions

  • Assuming you are randomly placed within the unit circle, what is the optimal path to get to the shore faster than your predator.
  • Assuming the predator runs 4 times as fast, what is the chance of you escaping? (Again assuming your placement is uniformly distributed within the unit circle)
N3buchadnezzar
  • 11,121
  • Does the predator have a choice as to whether to run around the circumference or to enter the water? Or is only one of allowed? If the predator is restricted to land, it is not even obvious that your optimal path is a straight line but you should always be able to escape if the speed ratio is $<4.603$, as shown at https://math.stackexchange.com/questions/31097/a-lady-and-a-monster/ – Henry Feb 08 '22 at 09:46
  • Meanwhile if the predator must be in the water, my unchecked calculations suggest your straight line escape path can depend on the speed ratio so will not always be either directly away from the predator or to the nearest land – Henry Feb 08 '22 at 09:51
  • @Henry the predator or monster has to stay on shore. I suspect you are correct as indicated in my last picture that the optimal path is somewhere along the blue line. I tried to optimize this, but it leads to some nasty calculations $\mathcal{L} = L - R/v$ which must be optimized both in terms of $\theta$ and $\rho$. Given that $L$ is the distance to the shore (straight line) and $R$ is the arclength. – N3buchadnezzar Feb 08 '22 at 09:52
  • If you see the linked question, it suggested a curved route initially (to get the swimmer away from the predator) followed by a straight line with the predator going the long way round the circle – Henry Feb 08 '22 at 09:54
  • Originally in my problem the speed difference between the swimmer and predator was variable $\nu$. Should I switch back to this if $4$ is trivial? I thought if $4$were solved I would be able to generalize the results. – N3buchadnezzar Feb 08 '22 at 09:55
  • In the linked question, there is a critical speed ratio of about $4.6033$. Below that, you can always escape. Above that, if there is an escape path then one would be a straight line perpendicular to the direction of the predator when it starts running running abound the circle and away from the the route the predator is taking, but note that the predator is going to have to run more than half the circumference (if the predator ever changes direction, you choose a new path starting from a better position) – Henry Feb 08 '22 at 10:24

0 Answers0