I have a multidimensional array $A_{ijkl}$ $\in\mathbb{C}^{m\times n\times o \times p}$ indexed by four integers $i,j,k,l$. I will call $i$ and $j$ the "left" indices, $j$ and $k$ the "up" indices, $k$ and $l$ the "right" indices, and $l$ and $i$ the "down" indices.
Given a fixed $A$, I am looking for the set of linear maps $P$ and $Q$ acting on the left and right indices which correspond to unitary linear maps $U$ acting on the up indices:
$B_{ijkl}=\sum_{\color{red}{\alpha\beta}\color{limegreen}{\mu\nu}}P_{ij\color{red}{\alpha\beta}}A_{\color{red}{\alpha\beta}\color{limegreen}{\mu\nu}}Q_{\color{limegreen}{\mu\nu}kl}=\sum_{\color{orange}{\beta\mu}}U_{\color{orange}{\beta}jk\color{orange}{\mu}}A_{i\color{orange}{\beta\mu} l}$
Where $U$ is unitary from up to down indices (i.e. when reshaped into a matrix like $U_{jk\rightarrow\color{orange}{\beta\mu}}$).
Here is the above equation in Penrose graphical notation, which may be clearer:
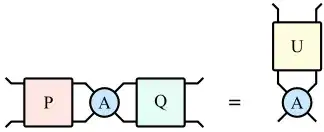
I am interested in this because I am trying to parameterize the subset of unitaries acting on the "up" indices of a given $A$ which decrease (or do not increase) its rank when viewed as a matrix from its left to right indices: $A_{ij\rightarrow kl}$. Initially, I assume that $A_{ij\rightarrow kl}$ may already be low-rank, and so considering the left/right acting $P$s and $Q$s made sense, because $\mathrm{rank}(PAQ)\leq \min\left(\mathrm{rank}(P),\mathrm{rank}(A),\mathrm{rank}(Q)\right)$.
In summary, I am asking:
- For a fixed $A$, are all rank-nonincreasing $U$s equivalent to some $P,Q$?
- For a fixed $A$, is there a way to restrict oneself to the manifold of $P,Q$s which correspond to $U$s?
I am pretty sure that (1.) is true, especially since (if I'm interpreting this paper correctly) for any rank-preserving linear transformation $T(A)$, $\exists$ $P$, $Q$ such that $T(A)=PAQ$ $\forall$ $A\in \mathbb{C}^{m\times n}$.
My main interest is question (2.). Any insight, or any better ways of parameterizing these rank-nonincreasing (ideally rank-decreasing) $U$s for a given $A$ would be much appreciated.