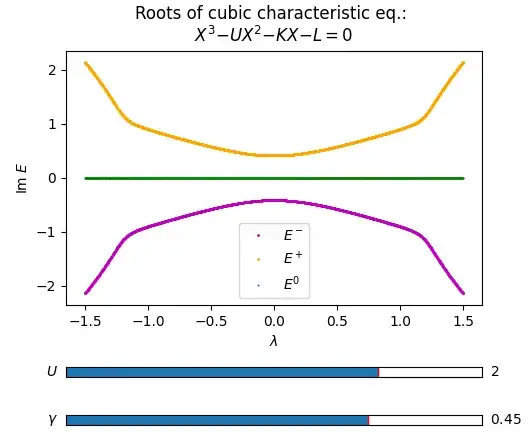
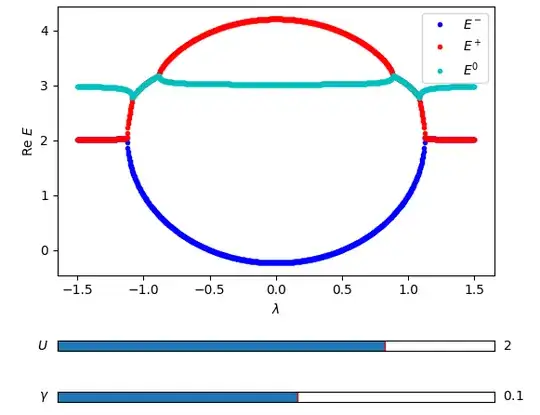
I have a cubic equation: $X^3-UX^2-KX-L=0$ (1)
with $X=1-E+U$, $K=4(1-\gamma^2-\lambda^2)$, $L=4\gamma^2U$.
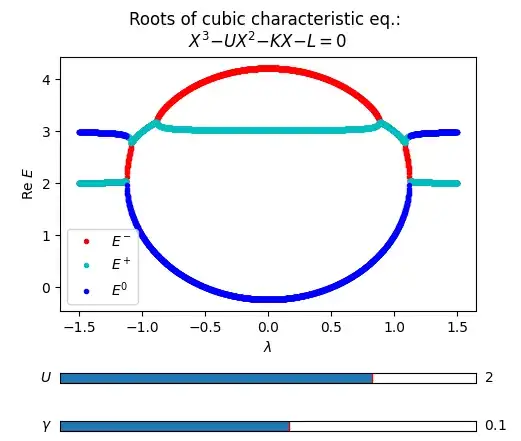
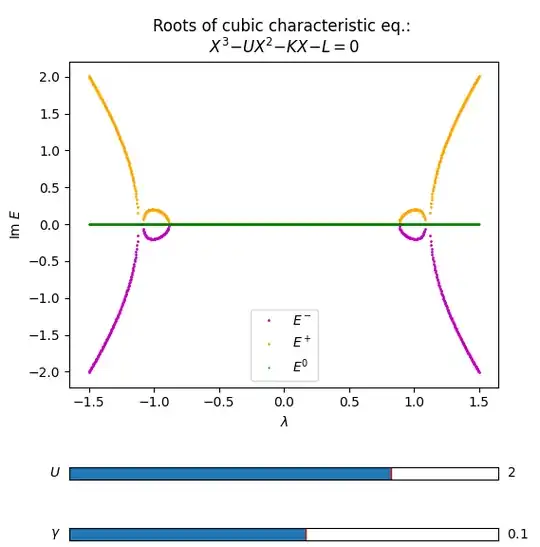
I solve Eq. (1) for the variable $E$ numerically for $U=2$ and different sets of parameter $\gamma =$ 0.1, 0.25, and 0.45 and plot real and imaginary parts of $E$ against $\lambda$. The real parts of the solutions for $X$ and $E$ differ by a constant shift for a fixed value of $U$ while the imaginary parts remain identical.
See the plots below. The plots plot all the roots or solutions. They are colored with three different colors by looking at the possible continuity of the roots or the solutions (here stressed on the continuity of the imaginary parts).
Here we see for the first case $\gamma = 0.1$, the continuity in the real parts of $E$ (Re $E$) break down while the imaginary parts (Im $E$) remain continuous for all parameter values of $\gamma$.
Since the solutions are found for discrete values of $\lambda$, we may think that extreme left and right of the cyan and blue curves of the first plot can be interchanged and hence made Re $E$ continuous all the way. However, that may lead Im $E$ to be discontinuous for other parameter values of $\gamma$ (I can add images if further clarity is needed).
How can we interpret or understand this? Or is there something fundamentally wrong?
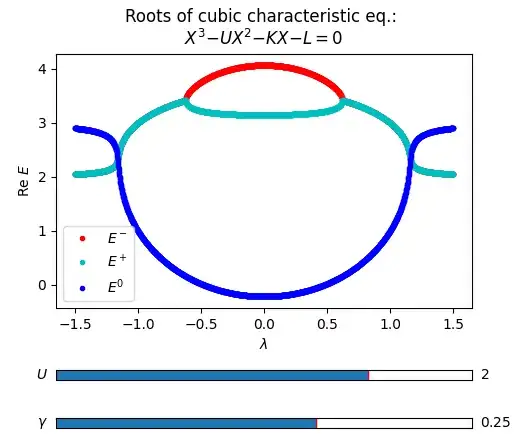
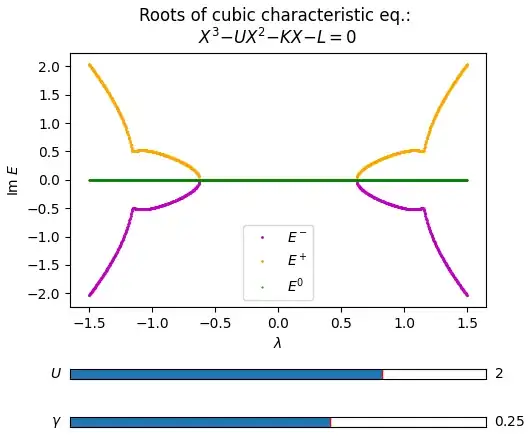
The alternative coloring for the first two plots could be the following (in this sense all the curves appear continuous function of $\lambda$).
Real part:
Imaginary part:
Though the above fixes the continuity issue, it appears that all three curves do not smoothly evolve with parameter $\gamma$. Experts' opinions awaited.