Thanks for the additional clarification. With this, I'll be able to write a full detailed proof of lemma $5$, sans the proof of the boundedness assumption which I'll cover in the other post.
Setup
$D^n$ is the space of $n$-dimensional cadlag adapted processes. We have $N \in D^n$, and semi-martingales $Z^1,\ldots ,Z^m$. Let $L^1(Z^j)$ denote the space of predictable and $Z^j$-integrable processes. Let $a_{ij} : D^n \to L^1(Z^j)$ be a map with the following property : for every $X,Y \in D^n$, $|a_{ij}(X) - a_{ij}(Y)| \leq K(X-Y)^*_-$ where $L_t^* = \sup_{s \leq t} \|L_s\|$ is the running maximum of $L$.
With this, define $F(X)$ for $X \in D^n$ component-wise by $$
F(X)_t^i = N_t^i + \sum_{j=1}^m\int_0^t a_{ij}(X)_tdZ^j
$$
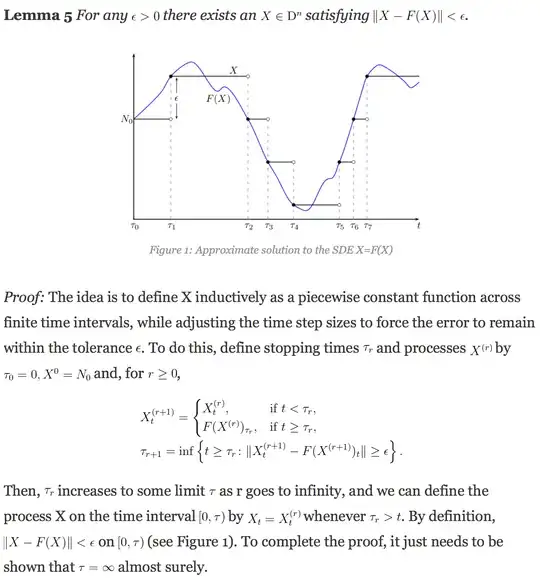
Lemma 5(Lowther) : For all $\epsilon>0$ there is an $X\in D^n$ with $\|X-F(X)\|< \epsilon$ i.e. $\|X_t - F(X)_t\|<\epsilon$ for all $t\geq 0$.
Reducing the proof to a proposition
The idea is to create $X$ as a jump process which remains constant across certain time intervals, within which it does not diverge from its $F$-value by more than $\epsilon$. We then require to prove that $X$ can be continued to infinity.
For this, we define the processes $X^r$ (which are successive extensions in time, finally giving $X$) using a sequence of stopping times $\tau_r$ (which indicate the time points at which the tolerance $\epsilon$ is breached and $X$ needs to jump). We have $X^0 = N_0, \tau_0=0$, and for $r\geq 0$,
$$
X^{r+1}_{t} = \begin{cases}
X^r_t & t < \tau_r \\
F(X^r)_{\tau_r} & t \geq \tau_r
\end{cases} \\
\tau_{r+1} = \inf\{t \geq \tau_r : \|X_t^{r+1} - F(X^{r+1})_t\| \geq \epsilon\}
$$
Note that the $\tau_r$ are increasing stopping times, which increase pointwise to some stopping time $\tau$ as $r \to \infty$. Let $X_t = X^r_t1_{\tau_r>t}$. We will show that $X$ is the desired process.
To begin, we show that on $[0,\tau)$ we have $\|X_t-F(X)_t\|<\epsilon$. Indeed, let $t<\tau$. Then, there exists $r$ such that $\tau_{r+1}>t \geq \tau_{r}$ so that $X_t = X^{r+1}_t$. Since $t<\tau_{r+1}$, by definition we have $\|X^{r+1}_t - F(X^{r+1})_t\| < \epsilon$. Since $X = X^{r+1}$ on $[0,t]$, it follows that $F(X)_t = F(X^{r+1})_t$ and therefore $\|X_t - F(X)_t\|<\epsilon$.
An integral formula
Let $\lambda_r \to 0$ be a sequence of positive reals, and let $M = 1_{[0,\tau)} (X-F(X))$ be the difference process that is bounded by $\epsilon$. For a process $Y$, we define the stopped process (at $\tau$) $(Y^\tau)_t = Y_{\tau \wedge t}$. With this, we now study the sequence of processes $\lambda_r X^{\tau_r}$, and show that it goes ucp to $0$.
We will ignore the $\lambda_r$ for now, and write some equalities that will hold on $[0,\tau)$. For one, note that $X^{\tau_r} = M^{\tau_r} + F(X)^{\tau_r}$. Hence, for every component $i$ we have $$
X^{i,\tau_r} = M^{i,\tau_r} + F(X)^{i,\tau_r} = M^{i,\tau_r} + N^{i,\tau_r} + \sum_{j=1}^m \int 1_{[0,\tau_r]}a_{ij}(X)dZ^j
$$
Write $a_{ij}(X) = a_{ij}(X) - a_{ij}(X_0) + a_{ij}(X_0)$ and note that $X_0=0$. This is done to invoke the difference property of the $a_{ij}$. With this, we get $$
X^{i,\tau_r}= \left(\sum_{j=1}^m \int 1_{[0,\tau_r]}(a_{ij}(X) - a_{ij}(0))dZ^j\right)+\left(M^{i,\tau_r} + N^{i,\tau_r} + \sum_{j=1}^m \int 1_{[0,\tau_r]}a_{ij}(0)dZ^j\right)
$$
Finally, we multiply by $\lambda_r$ to get $$
\lambda_rX^{i,\tau_r}= \left(\sum_{j=1}^m \lambda_r\int 1_{[0,\tau_r]}(a_{ij}(X) - a_{ij}(0))dZ^j\right)+\lambda_r\left(M^{i,\tau_r} + N^{i,\tau_r} + \sum_{j=1}^m \int 1_{[0,\tau_r]}a_{ij}(0)dZ^j\right)
$$
This doesn't perfectly match with Lowther, but it turns out we need not be very accurate.
ucp convergence
We will now show that both terms go to zero in ucp.
For the second, we begin by seeing that $\sup_{s \leq t} \|M_s\| <\epsilon$ for any $t$, therefore $\sup_{s \leq t} \|\lambda_rM_s\| <\lambda_r\epsilon \to 0$ as $r \to \infty$. The other two expressions can be resolved with the same idea.
Indeed, let $Y$ be any cadlag adapted process, and let $\sigma_r$ be a sequence of increasing stopping times with $\mu_r$ a sequence of positive reals converging to $0$. We can show that $\mu_rY^{\sigma_r} \to 0$ in ucp as follows : pick a $t,K$ and let $\epsilon>0$. Note that on $[0,t]$, because $Y$ has cadlag paths, it is a.s. bounded , see e.g. here. That is, we know that $$
P(\sup_{[0,t]} \|Y_s\| = \infty) = 0 \implies \lim_{L \to \infty} P(\sup_{[0,t]} \|Y_s\|> L) = 0
$$
Pick $L$ large enough so that $P(\sup_{[0,t]} \|Y_s\|> L)< \epsilon$. If this is true, then note that $\sup_{[0,t]} \|Y_s\| \geq \sup_{[0,t]}\|Y^{\sigma_r}_s\|$ for all $t$, therefore $P(\sup_{[0,t]} \|Y^{\sigma_r}_s\|> L)< \epsilon$ for all $r$, and multiplying by $\mu_r$ gives $P(\sup_{[0,t]} \|\mu_rY^{\sigma_r}_s\|> \mu_rL)< \epsilon)$ for all $r$. As $\mu_rL \to 0$, we can assume that $r$ is large enough so that $\mu_rL < K$. In that case, $$
P(\sup_{[0,t]} \|\mu_rY^{\sigma_r}_s\|> K)< \epsilon \forall \text{ large $r$} \implies \limsup_{r \to \infty}P(\sup_{[0,t]} \|\mu_rY^{\sigma_r}_s\|> K) < \epsilon
$$
for all $\epsilon>0$. Consequently, $\limsup_{r \to \infty}P(\sup_{[0,t]} \|\mu_rY^{\sigma_r}_s\|> K) \leq 0$, which forces $\lim_{r \to \infty}P(\sup_{[0,t]} \|\mu_rY^{\sigma_r}_s\|> K) = 0$, as desired.
Applying this with $\sigma_r = \tau_r$, and with each of $Y_t = N^i_t$ and $Y_t = \sum_{j=1}^m \int_0^t a_{ij}(0)dZ^j$ tells you that the second term goes in ucp to $0$.
For the first term (actually, I wonder if we can use the earlier argument instead of lemma 4, but that's a different topic) , we note that $\lambda_r|(a_{ij}(X) -a{ij}(0))| \leq \lambda_rKX^*_-$ by the difference property. Lemma $4$ applies straightaway since $\lambda_r$ is a convergent hence bounded sequence. It tells you that $\lambda_rX^{\tau_r} \to 0$ in ucp.
The existence of $\lim X_{\tau_r}$
We will now show that , providing $\tau<\infty$ has non-zero probability, $X_{\tau_r}$ has a limit with non-zero probability. We begin by writing the definition of $X_{\tau_r}$. Note that $X_{\tau_r} = X^{r+1}_{\tau_r} = F(X^r)_{\tau_r}$. Writing this down,
$$
X_{\tau_r} = N_{\tau_r} + \sum_{j=1}^m \int_0^{\tau_r} a_{ij}(X^r) dZ^j = N_{\tau_r} + \sum_{j=1}^m \int_0^{\tau_-} 1_{[0,\tau_r]}a_{ij}(X^r)dZ^j
$$
On $[0,\tau)$, we will now apply dominated convergence in probability. Indeed, $1_{[0,\tau_r]}a_{ij}(X^r) \to 1_{[0,\tau)}a_{ij}(X)$ a.s. by an argument similar to an earlier one in this answer. However, we also have $$
|1_{[0,\tau_r]}a_{ij}(X^r)| \leq |a_{ij}(X^r) - a_{ij}(0)| + |a_{ij}(0)|
$$
on $[0,\tau)$. The latter is integrable since $a_{ij}$ maps into $L^1(Z^j)$ for each $j$. The former is integrable since $|a_{ij}(X^r) - a_{ij}(0)| \leq K(X^r)^{*}_-$ which is a locally bounded hence $Z^j$-integrable function. It follows that $$
\lim_{r \to \infty} N_{\tau_r} + \sum_{j=1}^m \int_0^{\tau_-} 1_{[0,\tau_r]}a_{ij}(X^r)dZ^j
$$
exists, since $N_{\tau_r} \to N_{\tau^-}$. It follows that $\lim_{r \to \infty} X_{\tau_r}$ exists a.s., provided that $\tau<\infty$ i.e. the limit exists with non-zero probability.
Contradiction
However, $\lim_{r \to \infty} X_{\tau_r}$ doesn't exist a.s., since $$
X^r_{\tau_r} = F(X^{r-1})_{\tau_{r-1}} = X^r_{\tau_{r-1}} = X_{\tau_{r-1}}
$$
(the first and second equalities follow from the definition of $X^r$, the second from the definition of $X$) and $$
X_{\tau_{r}} = X^{r+1}_{\tau_{r}} = F(X^{r})_{\tau_r}
$$
Therefore $$
\|X_{\tau_r} - X_{\tau_{r-1}}\| = \|F(X^r)_{\tau_r} - X^r_{\tau_{r}}\| \geq \epsilon
$$
by the definition of $\tau_r$. Thus, $X_{\tau_r}$ is almost nowhere convergent, contradicting the conclusion of the previous section. The only possibility is that $\tau=\infty$, as desired.