$\int_{-\infty}^{\infty}\frac{1}{3 t^2+1} {\rm exp}\left(\frac{at^2+ibt}{3 t^2+1}+itx\right){\rm d}t$

Question

How to solve the integral?

$$ f(x)=\int_{-\infty}^{\infty}\frac{1}{3 t^2+1} {\rm exp}\left(\frac{a t^2+i b t}{3 t^2+1}+itx\right){\rm d}t\tag{1} \\{\rm with}\,\, x,b\in \mathbb{R},a\in\mathbb{R}_{<0},i^2=-1$$

This question was previously posted in Mathematica SE, however algorithms of Mathematica couldn't solve it. A deeper mathematical analysis is needed. In the solution a potpourri of Error function, Bessel function, hypergeometric function or infinite series of them can be expected (see these solved similar integrals: integral1, integral2, integral3).

A plot of $f(x)$ for $a=-200,b=-100$:

Answer 1

In a hurry, I pulled out of my head the equality of equations (1) & (2) but had no time to write down all the steps or reduce to simpler functions that seems to be possible with low effort. I leave that for other users.

$$\begin{align} f(x)&=\int_{-\infty}^{\infty}\frac{1}{3 t^2+1} {\rm exp}\left(\frac{a t^2+i b t}{3 t^2+1}+itx\right){\rm d}t\tag{1}\\ g(x)&=\frac{\pi e^{a/3}}{{\sqrt{3}}} \left( \begin{array}{l} \begin{array}{l} \sum _{k,v=0}^\infty \frac{c_-^k c_+^v}{k! (v!)^2}\left(\frac{-2x}{\sqrt{3}}\right)^{(k+v)/2}W_{(v-k)/2,-(k+v+1)/2}\left(\frac{-2x}{\sqrt{3}}\right) & x<0 \\ \sum _{k,v=0}^\infty \frac{c_-^k c_+^v}{(k!)^2 v!}\left(\frac{2x}{\sqrt{3}}\right)^{(k+v)/2}W_{(k-v)/2,-(k+v+1)/2}\left(\frac{2x}{\sqrt{3}}\right) & x>0 \\ \sum _{k,v=0}^\infty \frac{c_-^k c_+^v}{k! (v!)^2}(k+1)^{\overline{v}} & x=0 \\ \end{array} \end{array} \right)\tag{2} \end{align}$$

with $c_{\pm}=-\frac{a}{12}\pm\frac{b}{4 \sqrt{3}}$, rising factorial $(\cdot)^{\overline{v}}$, and Whittaker's $W$ function

$$W_{(k-v)/2,-(k+v+1)/2}(x)=\sqrt{\dfrac{x^{k-v}}{e^x}}\sum _{s=0}^k \binom{k}{s} \frac{(v+1)^{\overline{s}}}{x^s}\tag{3}$$ A comparison of $f(x),g(x),|f(x)-g(x)|$ for $a=-20,b=-10$ reveals numerical insufficiencies. They are higher for the example given in the question $(a=-200,b=-100)$.

Answer 2

$\color{brown}{\textbf{Useful integral.}}$

Denote $$f(k,m,x)=\int\limits_{-\infty}^\infty\dfrac {t^k}{(3t^2+1)^{m+k+1}}\,e^{itx} \,\text dt\tag1$$ Are known the integrals via the modified Bessel function $$f(0,m,x)=\sqrt{\dfrac\pi3}\,\dfrac{2}{m!}\,\left|\dfrac x{2\sqrt3}\right|^{m+\frac12}\operatorname K_{\large-\frac12-m}\left(\dfrac{|x|}{\sqrt3}\right),\tag2$$ $$f(1,m,x)=i\,\sqrt{\dfrac\pi3}\,\dfrac{x}{3(m+1)!} \,\left|\dfrac x{2\sqrt3}\right|^{m+\frac12}\operatorname K_{\large-\frac12-m}\left(\dfrac{|x|}{\sqrt3}\right)=\dfrac{ix}{6m+6}\,f(0,m,x).\tag3$$

Besides, $$f(k+2, m,x)=\int\limits_{-\infty}^\infty\dfrac {t^{k+2}}{(3t^2+1)^{m+k+3}}\,e^{itx} \,\text dt =\dfrac13\int\limits_{-\infty}^\infty\dfrac {(3t^2+1-1)\,t^k}{(3t^2+1)^{m+k+3}}\,e^{itx} \,\text dt,$$ $$f(k+2,m,x)=\dfrac13\big(f(k,m+1,x)-f(k,m+2,x)\big),$$ $$f(k+4,m,x)=\dfrac19\big(f(k,m+2,x)-2f(k,m+3,x)+f(k,m+4,x)\big),$$ $$f(2k,m,x)=\dfrac1{3^k}\sum\limits_{j=0}^k (-1)^j\dbinom k{j}f(0,m+k+j,x).\tag4$$ $$f(2k+1,m,x)=\dfrac{ix}{3^k}\sum\limits_{j=0}^k \dfrac{(-1)^j} {6(m+k+j+1)} \dbinom k{j}f(0,m+k+j,x).\tag5$$

In the Matematika language, $$\begin{align} &f(k,n+k+1,x)=\dfrac1{2\Gamma[1+k+n]}3^{-1-k} \bigg(3^{\large\frac12+\frac k2} \big(1+(-1)^k\big) \Gamma\left[\frac12+\frac k2\right]\\[4pt] &\times \Gamma\left[\frac12+\frac k2+n\right] \,\operatorname{HypergeometricPFQ}\left[\left\{\frac12+\frac k2\right\},\left\{\frac12,\frac12-\frac k2-n\right\},\frac{x^2}{12}\right]\\[4pt] &-I\, 3^{\large \frac k2} \big(-1+(-1)^k\big)\, x\, \Gamma\left[1+\frac k2\right]\, \Gamma\left[\frac k2+n\right]\\[4pt] &\times\operatorname{HypergeometricPFQ}\left[\left\{1+\frac k2\right\},\left\{\frac32,1-\frac k2-n\right\},\frac{x^2}{12}\right]\\[4pt] &+2\, I\, 3^{-n} |x|^{1+k+2 n} \Gamma[-1-k-2 n] \Gamma[1+k+n]\\[4pt] &\times\operatorname{HypergeometricPFQ}\left[\{1+k+n\},\left\{1+\frac k2+n,\frac32+\frac k2+n\right\},\frac{x^2}{12}\right]\\[4pt] &\times \left(\big(-1+(-1)^k\big) \cos\left[\frac {k\pi}2+n\pi\right] \operatorname{Sign}[x]+I \big(1+(-1)^k\big) \sin\left[\frac {k\pi}2+n\pi\right]\right)\bigg)\\ & \,\text{if}\; x\in\mathbb R\;\&\&\;\Re[k]>-1\;\&\&\;\Re[k+2 n]>-2 \end{align}\tag{$\Diamond$}$$

$\color{brown}{\textbf{Integration.}}$

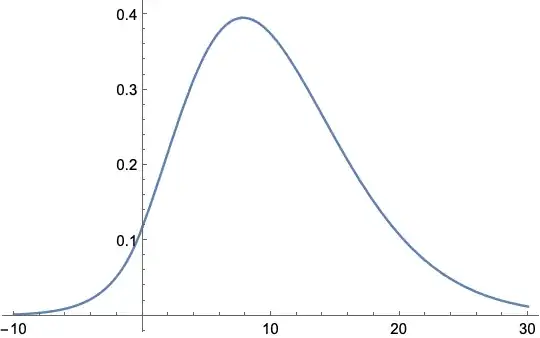
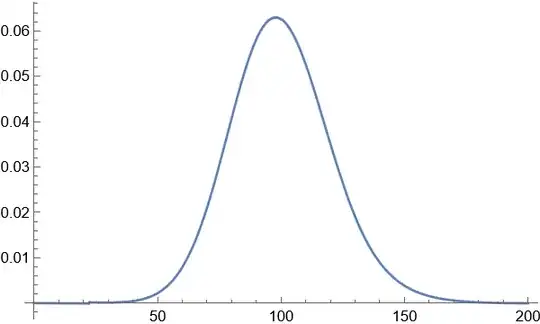
$$I=\int\limits_{-\infty}^\infty\dfrac{1}{3t^2+1}\,\exp\,\dfrac{at^2+ibt}{3t^2+1}\,\,e^{itx} \,\text dt$$ $$=\exp\,\dfrac a3\int\limits_{-\infty}^\infty\dfrac{1}{3t^2+1}\,\exp\left(-\dfrac{a}{3(3t^2+1)}\right)\exp\,\dfrac{ibt}{3t^2+1}\,\,e^{itx} \,\text dt$$ $$=\exp\,\dfrac a3 \sum\limits_{n=0}^\infty\dfrac1{n!}\left(-\dfrac a3\right)^n \sum\limits_{k=0}^\infty\dfrac{(ib)^k}{k!} \int\limits_{-\infty}^\infty\,\dfrac {t^k}{(3t^2+1)^{n+k+1}}\,e^{itx} \,\text dt,$$ $$I=\dfrac1{\sqrt3}\exp\,\dfrac a3 \sum\limits_{n=0}^\infty\dfrac1{n!}\left(-\dfrac a3\right)^n \sum\limits_{k=0}^\infty\left(-\dfrac13\right) ^{\large\genfrac\lfloor\rfloor{}{}{k+1}2}x^{^{\Large2\genfrac\{\}{}{}k2}} \,\dfrac{b^k}{k!}$$ $$\times \operatorname B\left(\genfrac\lfloor\rfloor{}{}{k+1}2+\dfrac12,n-\genfrac\lfloor\rfloor{}{}{1-k}2+\dfrac12\right)$$ $$\times\operatorname{_1F_2}\left(\genfrac\lfloor\rfloor{}{}{k+1}2+\dfrac12;\,\dfrac12+2\genfrac\{\}{}{}k2,\,\genfrac\lfloor\rfloor{}{}{1-k}2+\dfrac12-n;\dfrac{x^2}{12}\right),$$ 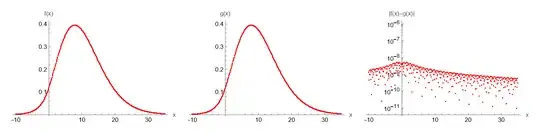and these approximations do not provide sufficient accuracy.

$\color{brown}{\mathbf{Alternative\ approach,\ case\; x=0.}}$

Since $$g(k)=\int\limits_{-\infty}^\infty\dfrac{(-a+3ibt)^k}{(3t^2+1)^{k+1}}\,\text dt =\sqrt{\dfrac\pi3}\,\dfrac{\Gamma\left(k+\frac12\right)}{k!}(-a)^k \operatorname{_2F_1}\left(\frac{1-k}2,-\frac k2;\frac12-k;\frac{3b^2}{a^2}\right),$$ then $$I\bigg|_{x=0}=\sqrt{\dfrac\pi3}\,\exp\dfrac a3\,\sum\limits_{k=0}^\infty \dfrac{\Gamma\left(k+\frac12\right)}{k!^2}\left(-\frac a3\right)^k \operatorname{_2F_1} \left(\frac{1-k}2,-\frac k2;\frac12-k;\frac{3b^2}{a^2}\right).$$

$\color{brown}{\textbf{Alternative approach, common case.}}$

$$I=\int\limits_{-\infty}^\infty\dfrac{1}{3t^2+1}\,\exp\,\dfrac{at^2+ibt}{3t^2+1}\,\,e^{itx} \,\text dt$$ $$=\exp\,\dfrac a3\int\limits_{-\infty}^\infty\dfrac{1}{3t^2+1}\,\exp\left(-\dfrac{a}{3(3t^2+1)}\right)\exp\,\dfrac{ibt}{3t^2+1}\,\,e^{itx} \,\text dt$$ $$=\exp\,\dfrac a3 \sum\limits_{n=0}^\infty\dfrac{a^n}{n!} \left(-\dfrac13\right)^n\sum\limits_{k=0}^\infty\dfrac{(ib)^{2k}}{(2k)!} \left(f(2k,n,x)+\dfrac{ib}{2k+1}\,f(2k+1,n.x)\right)$$ $$=2\sqrt{\dfrac\pi3}\exp\,\dfrac a3 \sum\limits_{n=0}^\infty\dfrac{a^n}{n!} \sum\limits_{k=0}^\infty\dfrac{b^{2k}}{(2k)!}\,\left(- \dfrac13\right)^{n+k} \sum\limits_{j=0}^k \dfrac{(-1)^j}{(n+k+j)!}\dbinom k{j}$$ $$\times\left(1-\dfrac{bx}{6(2k+1)(n+k+j+1)}\right) \left|\dfrac x{2\sqrt3}\right|^{n+k+j+\frac12} \operatorname K_{\large-\frac12-n-k-j}\left(\dfrac{|x|}{\sqrt3}\right).$$