Maximum number of edges in a balanced graph with n points, without small cycles (say, of length 2, 3, 4)

Question

Let's say we have $n$ points numbered from $1$ to $n$.

What is the maximum number of directed edges possible on a graph with these $n$ points:

• without any cycle of length $\leq k$, for example without cycles of length 2, 3, 4

• such that the number of edges arriving on all points are "balanced". More precisely, if we note $N(j)$ the number of edges arriving on the point $j$, we want that:

  $$\frac{\max_{1 \leq j \leq n} N(j)}{\min_{1 \leq j \leq n} N(j)} \leq 2, \qquad \textrm{ or any other constant i.e. }O(1)$$

Even if we don't find the exact maximum, how could we find an estimate?

---

Notes:

The idea for the 2nd bullet point is that we want $(N(j))_{1 \leq j \leq n}$ to be uniformly distribued among all points, i.e. we don't want a point that receives hundreds of incoming edges, whereas another point receives nearly no incoming edge at all!

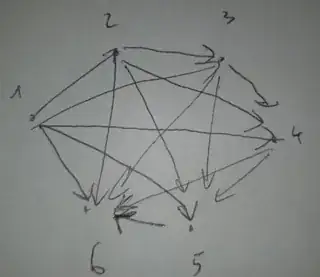
For example the answer of Maximum number of edges in a directed graph on $n$ vertices without cycles is not satisfying because, here with $n=6$,

• 5 edges arrive on point #6
• 0 edges are arriving on point #1

so here $\max N(j) / \min N(j) = +\infty$.

Also Maximum number of edges of a planar graph without cycles of length 3 and 4 seems linked but doesn't give any solution or construction for a solution when $n$ is large.

Answer 1

I can't find the exact maximum, but I can proof the following match bounds (that is, up to a constant time): if there is no $k$-cycle, and $\frac{\max_{1 \leq j \leq n} N(j)}{\min_{1 \leq j \leq n} N(j)}\le l$, suppose the maximum number of edges be $E$, then we have

$$\frac{n^2l}{8k}+O(n)\le E\le \frac{3n^2l}{2k}$$

for $l\le k/3$.

The construction for lower bound: suppose the vertices are split into sets $X_1,X_2,\dots,X_m,X_{m+1},X_{m+2},\dots,X_{k+1}$ such that $|X_1|=|X_2|=\dots=|X_m|=\frac{nl}{2k}$ and $|X_{m+1}|=|X_{m+2}|=\dots=|X_{k+1}|=\frac{n}{2k}$. Let $m=\frac{k}{l}$. We ignore the remainders. Therefore, we can give a graph go from $X_i$ to $X_{i+1}$ (indices modulo $k+1$), and we have $E\ge (m-1)(\frac{nl}{2k})^2\ge \frac{k}{2l}(\frac{nl}{2k})^2=\frac{n^2l}{8k}$.

The proof for upper bound: From a point $v$, we do backward BFS. That is, we have $A_1,A_2,\dots,A_k$ be the sets of vertices TOWARDS $v$ in distance $1,2\dots,k$, respectively. We know that the indegree of $A_i$ only comes from $A_i$ itself or $A_{i+1}$. If it has indegree after $A_{i+1}$, this violates the property of BFS. If it has indegree before $A_i$, there is a cycle no longer than $k$. Let $X=V\backslash \bigcup_{i=1}^k A_i$ ($V$ is the vertex set), and the indegree to $A_k$ must come from $A_k$ or $X$. So we have the minimum indegree for the vertices in $A_i$ is no more than $|A_i|/2+|A_{i+1}|$, and the minimum indegree for the vertices in $A_k$ is no more than $|A_k|/2+|X|$. So, the minimum indegree of the vertices in $A_1,\dots,A_k$ is no more than the average, that is, $\frac{1}{k}(\sum_{i=1}^{k-1}|A_i|/2+A_{i+1}+|A_k|/2+|X|)\le \frac{3n}{2k}$. Therefore, the indegree is no more than $3nl/2k$ for each vertex, and thus the total number of edges is $3n^2l/2k$.

For $l\ge k/3$, we give a lower bound of $\frac{n^2l^2}{2(l+k)^2}+O(n)$. We again split the vertices into $X_1=Y_1,X_2,\dots,X_{l+1}=Y_2, Y_3,\dots,Y_{k+1}$ such that all the sets are having $\frac{n}{k+l}$ vertices (we still ignore the remainders). Then we connect all the edges from $X_i$ to $X_j$ for $1\le i<j\le l+1$, and all edges from $Y_i$ to $Y_{i+1}$ (indecis modulo $k+1$.) So the total number of edges is $(\frac{n}{k+l})^2(\frac{l(l+1)}{2}+k)=\frac{n^2l^2}{2(k+l)^2}$.