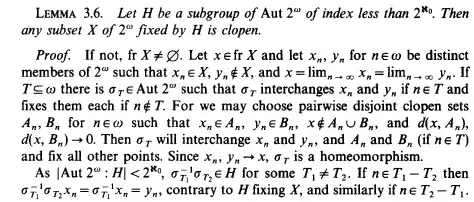The following is an excerpt of Truss's 1989 paper Infinite Permutation Groups II.: Subgroups of Small Index. (The transcript will appear later.)
Here, $2^\omega$ the Cantor space, automorphisms mean autohomeomorphisms, and I take "fr" to mean "the frontier" or the boundary.
His argument is convincing, but I have a small issue here: What if the complement of $X$ is finite? Then we wouldn't be able to pick distinct $y_n$ in $2^\omega \setminus X$. I tried to argue that $H$ is too big (so to speak) to result in such a situation by computing the the order or the index of the stabilizer of $2^\omega \setminus H$ but to no avail.