4

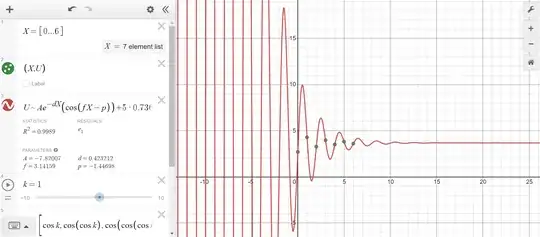
What function would one use to describe $k$ iterations of $\cos(n)$? I'm pretty sure that the function would be a damped sine wave (as can be seen in the curve fit equation I wrote in the third row), however the actual formula is probably quite complicated as it involves the Dottie number, which, to my knowledge, cannot be expressed in terms of $e$, $\pi$, or polynomial roots.

Below is an attempt of curve-fitting on $n=1$. Some of the deficiencies of this fit I've noticed while experimenting with Desmos are that the lines are far too steep (even without the scale factor or with a smaller scale factor), and the fit seems to be weaker for even $n$ (although I presume that this is simply an artifact of approximation). Note that the y-axis has been scaled by a factor of 5 for the sake of graph readability.

Graph on Desmos

Josh
  • 477
  • 1
    $x \mapsto \cos(\cos(...\cos(x) ...))$ must be $2 \pi $ periodic at least. – copper.hat Jan 14 '22 at 23:17
  • Care to explain? I'm not looking for the result of infinite iterations of $\cos(x)$, because that's obviously the Dottie number. I'm talking about a finite number of iterations, namely $k$ iterations. – Josh Jan 15 '22 at 01:14
  • The above is meant to have $k$ applications. If the innermost function is periodic then the $k$ fold application must be too, it follows almost by definition. – copper.hat Jan 15 '22 at 01:29
  • Notating this function as $f(n,k)$, $f(1,0)$ would be 1. $f(1,1)$ would be $\cos(1)$. $f(1,2)$ would be $\cos(\cos(1))$, and so on. Likewise, $f(2,1)$ would be $\cos(2)$, $f(2,2)$ would be $\cos(\cos(2))$, etc. – Josh Jan 15 '22 at 01:52
  • Yes, I got that :-). – copper.hat Jan 15 '22 at 01:53
  • Just plot $\cos x, \cos(\cos x)$, etc. in Dismos. – copper.hat Jan 15 '22 at 01:54
  • 1
    https://www.wolframalpha.com/input/?i=plot+cos%28x%29+and+cos%28cos%28x%29%29+and+cos%28cos%28cos%28x%29%29%29+and+cos%28cos%28cos%28cos%28x%29%29%29%29+and+cos%28cos%28cos%28cos%28cos%28x%29%29%29%29%29 – Aaron Hendrickson Jan 15 '22 at 02:24
  • According to this video, $\lim_{n\to\infty}f(x,n)=0$ for any $x\in\Bbb R$. – Aaron Hendrickson Feb 16 '22 at 11:47
  • Little graph that might help: https://www.desmos.com/calculator/tkcezsn5zy – Einsteinium May 14 '24 at 06:05

2 Answers2

2

The limit $\lim_{k\to\infty}\cos^{(k)}(x)$ ($k$ iterations of $\cos$ applied to $x$) is equal to $\xi$, where $\xi$ is a solution to the equation $\cos\xi=\xi$. It is independent of $x$. Therefore for large $k$, you will have lots of oscillations in a small strip around the line $y=\xi\approx 0.739$.

uniquesolution
  • 18,982
0

If you look at $\cos(\cos(\cos(x)))$, you’ll see that it’s periodic with period $\pi$. In particular, it looks something like $a \cos(2x)+b$ for some constants $a$ and $b$. In the limit $a$ will geometrically converge to 0 at approximately $\sin(\xi)^k$ while $b$ is $\xi$ such that $\xi=\cos(\xi)$.

Eric
  • 8,378
  • I think you're misunderstanding my question. What I mean is, the x axis is the number of iterations (k), and the y axis is the result when applied to n. – Josh Jan 15 '22 at 04:25