pdf of a random variable involving distances

Question

Let $x_1,x_2,x_3,\dots,x_n$ be n points on the unit segment $[0,1]$.Let $X$ be a uniformly and randomly chosen point in $\in[0,1]$ and $$Y= \Bigg|\frac1n \sum_1^n|X-x_i|-\frac12 \Bigg |.$$ Is it psossible to find the pdf of $Y.$Thank you for any hints/suggestions in advance.

Answer 1

I would like to give here an important intermediate result. Up to you to use it for reaching the final objective.

The set of $n$ values $x_i$ being fixed ($n$ being assumed an odd integer), Let us in a first step define the function

$$f(x):= \frac{1}{n}\sum_{1}^n|c-x_i|$$

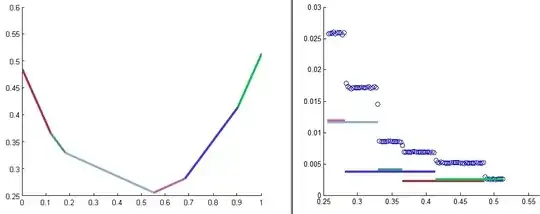
(see the graph of such a function on the left of the following figure ; the abscissa of the minimum is the median of values $x_i$). Let us now define the random variable

$$Z=f(U), \ \ \ \ U \sim Unif(0,1)$$

The pdf of $Z$ has the shape of a decreasing staircase as can be seen on the right hand part of the figure which represents a histogram (materialized by little circles) of the values taken by $Z$ in a large scale simulation (you can consult as well the Matlab program having generated the left and right figure below).

The reason is that this pdf is the sum of $n+1$ weighted characteristic functions of intervals to be found on the axis of ordinates of the first figure, colors having been chosen in order that one can retrieve on the right figure the origin of these characteristic functions on the left figure.

I will stop my explanations here, waiting for the OP to say if he/she has understood the origin of the different "characters" leading to the result.

Remark: in the case where the number of points is even, function $f$ has a "plateau" instead of a peaky minimum. As a consequence, the pdf of $Z$ has a staircase shape, like above, to which must be added a $\delta$ function.

Matlab program:

clear all;close all;hold on;
LS='linesmoothing';LW='linewidth';
A=[0.12,0.18,0.55,0.68,0.9];
n=length(A);
f=@(x)(sum(abs(bsxfun(@minus,x'*ones(1,5),A)),2));
x=0:0.01:1;
figure(1);set(gcf,'color','w');plot(x,f(x)/n,LS,'on',LW,1);
col=rand(n+1,3);% colors' table
B=[0,A,1];C=f(B)/n;
for k=1:n+1;
    plot(B(k:k+1),C(k:k+1),'color',col(k,:),LS,'on',LW,3);
end;
m=3000000;x=rand(1,m);
figure(2);hold on;set(gcf,'color','w');
[U,V]=hist(f(x)/n,100);
scatter(V,U/m);
for k=1:n+1;
    h=(B(k+1)-B(k))/(abs(C(k)-C(k+1))*85*n);
    plot([C(k),C(k+1)],h*[1,1],'color',col(k,:),LW,3);
end