The sketch given below might help you.
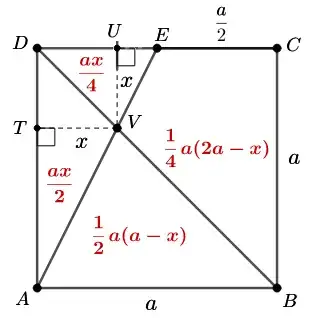
$\underline{\text{Added at the request of @Utkarsh}}$
Let us denote the point of intersection of $AE$ and $BD$ as $V$. We draw a line segment perpendicular to the side $AB$ through $V$ to cut the side $CD$ at $U$. Another line segment is drawn through $V$ perpendicular to the side $AD$ to meet it at $T$. For brevity, we let $AB = BC= a$, and $VT = x$.
Area of $\triangle DAV$ can be expressed as,
$$\text{Area of }DAV = \frac{1}{2}ax. \tag{1}$$
The area of $\triangle ABD$ is equal to the half of that of $\square ABCD$. Therefore,
$$\text{Area of }ABD = \frac{1}{2}a^2. \tag{2}$$
Using (1) and (2), we can determine the area of $\triangle ABV$ as,
$$\text{Area of }ABV = \text{Area of }ABD - \text{Area of }AVD = = \frac{1}{2}a^2 - \frac{1}{2}ax = \frac{1}{2}a \left(a-x\right). \tag{3}$$
Since $V$ is located on the diagonal of $\square ABCD$, $VU = VT = x$. This let us express the area of $\triangle EDV$ in terms of $a$ and $x$ as shown below.
$$\text{Area of }EDV = \frac{1}{4}ax \tag{4}$$
An expression for the area of the quadrilateral $BCEV$ can be derived using (4).
$$\text{Area of } BCEV = \frac{1}{2}a^2 - \frac{1}{4}ax = \frac{1}{4}a \left(2a-x\right) \tag{5}$$
Now, we need to find $x$ in terms of $a$. To do that consider the two similar triangles $EDV$ and $ABV$. According to the theorem Euclid VI. 19., the ratio of the areas of two similar triangles is equal to the ratio of the squares on any of the three pairs of corresponding sides. Therefore, we shall write,
$$\text{Area of }EDV : \text{Area of }ABV = DE^2 : AB^2 = \frac{1}{4}a^2 : a^2 = 1: 4.$$
We can express the same ratio using (3) and (4) as,
$$\text{Area of }EDV : \text{Area of }ABV = \frac{1}{4}ax : \frac{1}{2}a \left(a-x\right) =x : 2 \left(a-x\right). $$
Therefore,
$$\dfrac{x}{2 \left(a-x\right)}=\dfrac{1}{4} \qquad\longrightarrow\qquad x=\dfrac{1}{3}a.$$
We use this to eliminate $x$ in formulae (1), (3), (4), and (5) to get,
$$\text{Area of }DAV = \dfrac{1}{6}a^2, \quad \text{Area of }ABV = \dfrac{1}{3}a^2, \quad \text{Area of }EDV =\dfrac{1}{12}a^2, \quad\text{and}\quad$$ $$\text{Area of } BCEV = \dfrac{5}{12}a^2.$$