0

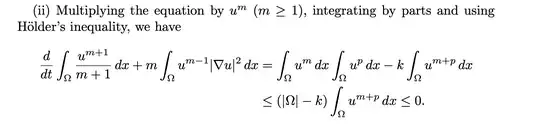
In the book Superlinear Parabolic Problems Blow-up, Global Existence and Steady States, page 492 this equation appears in which the book says it uses Holder inequality enter image description here

My question is whether it's really possible to use Holder this way, that is (Here $|\Omega|< \infty$):

$$ \int_{\Omega}u^{m}dx \int_{\Omega}u^{p}dx \leq |\Omega| \int_{\Omega}u^{m+p}dx$$

I've tried using Classic Holder inequality and this reverse version Reverse Holder Inequality $\|fg\|_1\geq\| f\|_{\frac{1}{p}}\|g\|_{-\frac{1}{p-1}}$ , but nothing comes close to what the book says. Another thing is that the book does not assume anything about $m$ before making this inequality, only later it says that $m+1 \geq p$

Ilovemath
  • 3,176
  • 1
    Use Hölder with exponents $r = (m + p)/m$ and $r' = (m+p)/p$ to get $\int u^m\le |\Omega|^{p/(m+p)}\int u^{m+p}$. The other is similar. – user90189 Dec 30 '21 at 17:24
  • 1
    thank you, it worked, there was only one thing missing, which was the power $\dfrac{m}{m+p} $in the integral $\int u^{m+p}$. – Ilovemath Dec 30 '21 at 19:02

0 Answers0