The standard configuration of Brunnian "rubberband" loops shows a series of unknots each bent into a U-shape, with their ends looped around the middle of the next unknot, as shown here (drawn by David Epstein) Brunnian rubberband loop object:
This has the defining Brunnian link property that all elements are interlocked, but the removal of any element causes all the others to disentangle. But it requires each element to link to the next with 8 cross-overs, and be bent around so as to form a minimum of four bights along its "length".
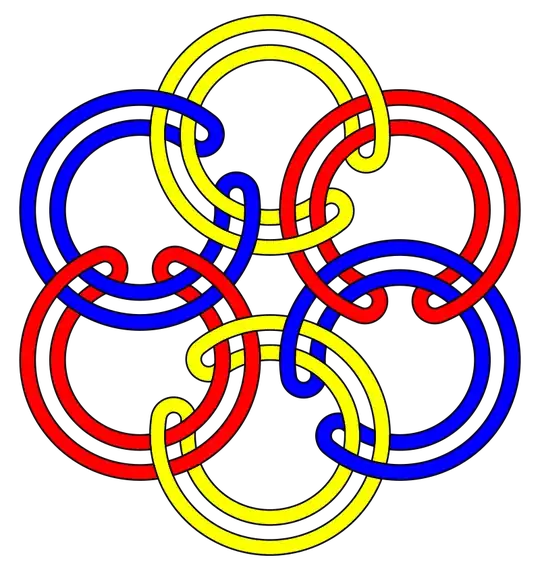
I have been playing around with an object that I call an "exaltation of larks", since it is based on lark's-head knots to connect the elements. This reduces the number of cross-overs to 6 per pair, and allows for each element to have only two bights along its length. A visual is here exaltation of larks object:
This also seems to fulfill the Brunnian definition, and is substantially simpler. I am wondering if (1) this object is already known and has another name, and/or (2) the object is not Brunnian for some reason I have overlooked. Thanks! (First time here...)
Added 12/22/21:
I've done a pretty good look-back in the papers at this point, and here's what I've come up with. Dale Rolfsen describes a Brunnian link which is equivalent to a five-element "exaltation of larks" (p. 69, exercise 15, Knots and Links, 1976). This is cited directly in at least one other place ("New Criteria and Construction of Brunnian Links" by Sheng Bai and Weibiao Wang https://arxiv.org/pdf/2006.10290.pdf). None of those authors note that this is a simpler version of the Brunnian chain than the standard, and most compendiums of Brunnian links do not show this pattern at all.
So I think I have what I need here, thanks for the help!