The only situation this would be true if there exists a constraint that causes degeneracy in a model where one of the basic variables has a zero as its right-hand-side value, and thus doesn’t contribute to a model upon a pivot. For example:
Suppose we have a model:
$$\text{min }z=-x_1+x_2-x_3$$
Subject to,
$$x_1+x_2\le 4$$
$$-x_2+x_3\le0$$
$$x_1,x_2,x_3 \ge0$$
Converting this to standard form, we get:
$$\text{min } z +x_1 - x_2 +x_3 = 0$$
Subject to:
$$x_1+x_2+s_1=4$$
$$-x_2+x_3+s_2=0$$
$$x_1, x_2, x_3, s_1, s_2 \ge0$$
From here, lets put this in a tableau:
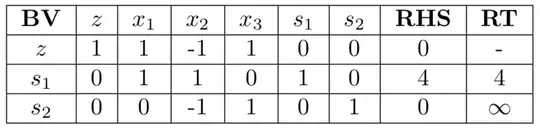
Let’s pivot the $x_1$ column to produce:
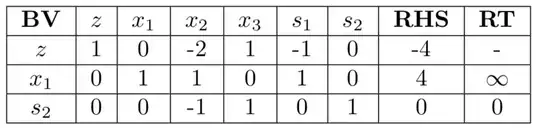
Then lets pivot the $x_3$ column to produce our final tableau:
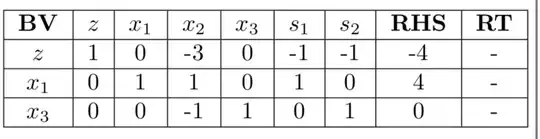
Notice that the solution produced in the second tableau is optimal, $(4,0,0)$, and is exactly the same as the solution produced by the third tableau. In addition, the second tableau produced an optimal solution, but had a $C^\pi_j > 0$, which shows that the simplex method doesn’t terminate right away.
Here’s a PowerPoint slide I found that explains more on Degeneracy in models.


