5

While I was observing some houseflies around, I wondered what is the probability that at least one triplet of them chosen will fall under the same straight line. I made some assumptions so as to remove "infinity" from the picture. Firstly, let $a$ denote the area occupied by one "housefly" (point) and $A$ denote the area of square plane considered. Total number of points (lattice points) is $\lfloor \frac{A}{a} \rfloor$. Let $n$ denote number of points in one side of the square plane. $n = \sqrt{\lfloor \frac{A}{a} \rfloor}$. 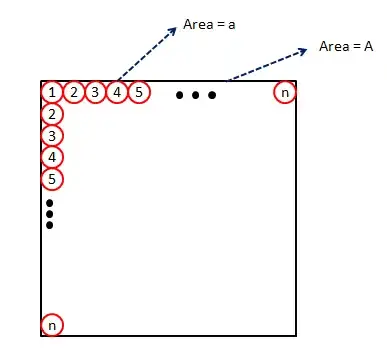scenario

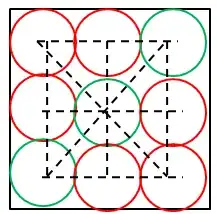
I started from a very simple case. Let us consider a square with $3$ points on its sides. Let me assume that only $3$ points are chosen. For $3$ of them to fall on a straight line is equivalent to chosing $3$ points from any fixed straight line.

case1

Since there are $8$ straight lines containing $3$ points, so total number of favorable selections is ${3 \choose 3} . 8 = 8$ and total possible selections is $ {9 \choose 3} = 84$. Therefore Probability $= 0.095$ . Let us now consider a square with $4$ points on its sides. Let me assume that only $3$ points are chosen.

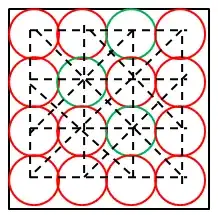
case2

Since there are $10$ straight lines containing $4$ points and $4$ straight lines containing $3$ points, so total number of favorable selections is ${4 \choose 3}.10 + {3 \choose 3}.4 = 44$ and total possible selections is ${16 \choose 3} = 560$. Therefore probability $= 0.078$ . Let us now consider a square with $5$ points on its sides. Let me assume that only $3$ points are chosen.

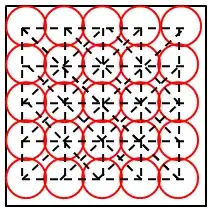
case3

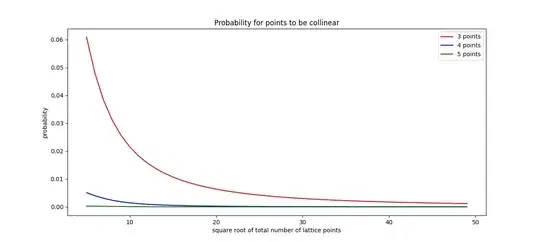
Since there are $12$ straight lines containing $5$ points, $4$ straight lines containing $4$ points and $4$ straight lines containing $3$ points, so total number of favorable selections is ${5 \choose 3}.12 + {4 \choose 3}.4 + {3 \choose 3}.4 = 140$ and total possible selections is ${25 \choose 3} = 2300$. Therefore probability $= 0.0608$ . Generalizing this idea we get, $$P(n) = \frac{{n \choose 3}.(2n+2) + ({n-1 \choose 3}+{n-2 \choose 3}+...+{3 \choose 3}).4}{{n^2 \choose 3}}$$ or $$\boxed{P(n) = \frac{{n \choose 3}.(2n-2) + {n+1 \choose 4}.4}{{n^2 \choose 3}}}$$ where $P(n)$ denotes the probability that $3$ points chosen in a plane with lattice points $n^2$ will be collinear. Generalizing this idea to choosing $r$ points, probability that all $r$ points lie on the same straight line is $$P(n,r) = \frac{{n \choose r}.(2n-2) + {n+1 \choose r+1}.4}{{n^2 \choose r}}$$

The $P(n)$ vs $n$ graph is plotted below: probability1

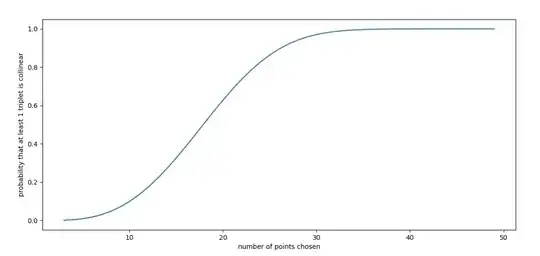
Now, coming to the final part of the question, let $x$ denote the total number of points chosen. Total number of triplets is ${x \choose 3}$. The chances of each triplet being collinear is given by $P(n)$. Therefore using the concept of probability, it can be concluded that probability that at least one triplet of points chosen will fall under the same straight line $$\boxed{P'(n) = 1 - (1-P(n))^{x \choose 3}}$$ Here is a $P'(n)$ vs $x$ graph for $n = 100$. The "strange" thing is that probability approaches $1$ for $x>30$. Does that mean if we choose 30 points out of only $100^2$ lattice points we may not be able to make a 30-sided polygon?

Am I correct in my deductions?

final_curve

N.B.: This question is different from this because I am not dealing with "infinity".

S Das
  • 501
  • Can houseflies only ever occupy the centers of the circles? – 5xum Dec 15 '21 at 13:03
  • $n$ is the number of circles (lattice points) in one side of the square (see the first part). In the last part, I mean to say that when lattice points in the plane is $100^2$ then, if any 30 or more points are chosen out of those lattice points then it is very likely that at least 1 triplet will be collinear (i.e. choosing 30 points out of only $100^2$ lattice points we may not be able to make a 30-sided polygon) . Is it really so ?--- is my question. – S Das Dec 15 '21 at 13:29
  • The position (space) occupied by a housefly is denoted by a circular region. It can be related to this: imagine a dot made with a pen on a paper. That dot is the circle. – S Das Dec 15 '21 at 13:32
  • Yeah I dunno. You can run a Python/program simulation and check. Also, I think the question would be better if it just referred to points on a lattice and not circles. – Adam Rubinson Dec 15 '21 at 14:26
  • 1
  • The events that $p_1, p_2, p_3$ and $ p_3, p_4 , p_5$ form lines is not independent. I suspect they are positively correlated. 2) For the final part, just because 3 out of 30 of the chosen points form a line, doesn't imply that those 3 must be consecutive vertices which disallows the polygon. We are only guaranteed that we can't form a polygon when 21 points are on the same line (as then we can show that 3 of them are consecutive).
    • – Calvin Lin Dec 15 '21 at 16:09