The parametric equation of the ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 $ is
$ r = (x, y) = ( a \cos t , b \sin t ) \hspace{20pt} t \in \mathbb{R} $
Now $P_1 = (x_1, y_1) = (a \cos t_1, b \sin t_1 ) $
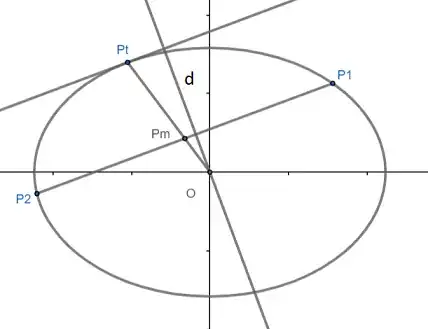
Suppose $Q = (a \cos s, b \sin s)$ is the point where the tangent is to be drawn.
The unit normal vector at $Q$ is
$n = \dfrac{(b \cos s , a \sin s )}{\sqrt{b^2 \cos^2 s + a^2 \sin^2 s}} $
The distance between the tangent line and the line $P_1 P_2 $ that is parallel to it is
$(P_1 Q) \cdot n = \dfrac{ ab( (\cos s - \cos t_1 ) \cos s + (\sin s - \sin t_1 ) \sin s ) }{\sqrt{b^2 \cos^2 s + a^2 \sin^2 s}} = d $
Simplifying,
$(P_1 Q) \cdot n = \dfrac{ ab( 1 - ( \cos t_1 \cos s + \sin t_1 \sin s )) }{\sqrt{b^2 \cos^2 s + a^2 \sin^2 s}} = d $
Therefore,
$ d {\sqrt{b^2 \cos^2 s + a^2 \sin^2 s}} = a b( 1- ( \cos t_1 \cos s + \sin t_1 \sin s ) ) $
Squaring,
$ d^2 (b^2 \cos^2 s + a^2 \sin^2 s ) = a^2 b^2 ( 1 + \cos^2 t_1 \cos^2 s + \sin^2 t_1 \sin^2 s + \dfrac{1}{2} \sin 2 t_1 \sin 2 s - 2 ( \cos t_1 \cos s + \sin t_1 \sin s ) ) $
After using the identities $\cos^2 s = \frac{1}{2} (1 + \cos 2 s ) $ and $\sin^2 s = \frac{1}{2} (1 - \cos 2 s)$, the last equation becomes of the form
$A \cos s + B \sin s + C \cos 2 s + D \sin 2 s + E = 0 $
where
$A = 2 a^2 b^2 \cos t_1 $
$B = 2 a^2 b^2 \sin t_1$
$C = -\dfrac{1}{2} \left((a b) ^ 2 \cos(2 t_1) - d ^ 2 (b ^ 2 - a ^ 2) \right) $
$D = -\dfrac{1}{2} a^2 b^2 \sin(2 t_1) $
$E = \dfrac{1}{2} d ^ 2 (a ^ 2 + b ^ 2) - \dfrac{3}{2} a ^ 2 b ^ 2$
Which can be solved for $s$, using the substitution $z = \tan \dfrac{s}{2} $ that results in a quartic polynomial equation in $z$.
Once $s$ is found (there will be two solutions), the equation of the line $P_1 P_2 $ is
$ n \cdot ((x, y) - P_1) = 0 $
where $n = ( b \cos s, a \sin s ) $
This line we need to intersect with the ellipse to find $P_2$. This can be done as follows. Since $(x, y)$ is on the ellipse then $P_2 =(x_2, y_2) = (a \cos t_2 , b \sin t_2)$. Substitute this into the equation of the line, you get,
$ (b \cos s , a \sin s ) \cdot ( a (\cos t_2 - \cos t_1) , b (\sin t_2 - \sin t_1) ) = 0 $
Dividing through by $ ab $,
$ \cos s (\cos t_2 - \cos t_1) + \sin s (\sin t_2 - \sin t_1 ) = 0 $
In which $t_1$ and $s$ are known, and the unknown is $t_2$. This equation is of the form
$ \cos(t_2 - s) = \cos(t_1 - s) $
Since $t_2 \ne t_1$ then
$ t_2 - s = - (t_1 - s) $
from which,
$ t_2 = 2 s - t_1 $
and $P_2 = (a \cos t_2, b \sin t_2 ) $
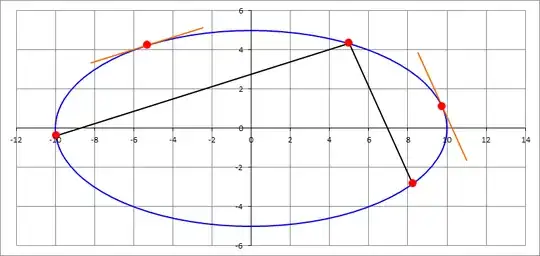
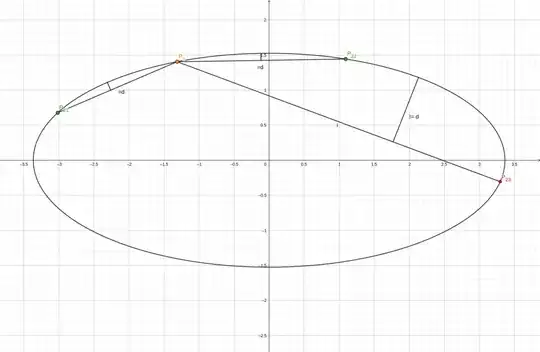
As a numerical example, I've taken the ellipse with $a = 10, b = 5, t_1 = \dfrac{\pi}{3}$ and the distance $d = 3 $. The figure below shows the two solutions.