4

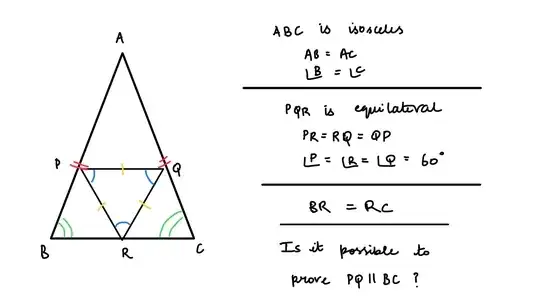
View diagram here

Triangle $ABC$ is isosceles. An equilateral triangle $PQR$ is inscribed in it with $R$ being the midpoint of $BC$. How can you prove $PQ \parallel BC$?

user21820
  • 60,745
Afsheen
  • 45
  • 6
  • Joining $AR$ might help. – RiverX15 Nov 27 '21 at 07:23
  • @RiverX15, I tried that but I didn’t get anywhere – Afsheen Nov 27 '21 at 07:35
  • It's obvious that $BP = CQ$ – Math Lover Nov 27 '21 at 08:01
  • @MathLover Well, the altitude of an isosceles triangle is its median and its angle bisector (of angle A) so I tried something with that but I got nowhere. And yes I can see that BP=CQ but I would be grateful if you could prove it for me, thanks. – Afsheen Nov 27 '21 at 08:07
  • 1
    @MathLover Actually, it's not necessarily true $BP = CQ$ based on just the information provided. Using the law of sines in $\triangle BRP$ and $\triangle CQR$ shows that $\sin(\measuredangle CQR) = \sin(\measuredangle BPR)$, so either $\measuredangle CQR = \measuredangle BPR$ or $\measuredangle CQR + \measuredangle BPR = 180^{\circ}$. In the former case, you are correct but, in the latter case, one can show that $\measuredangle PBR = \measuredangle QCR = 30^{\circ}$, with it then being possible to have $PB \neq CQ$ and $PQ \not\parallel BC$. The diagram then would appear quite different. – John Omielan Nov 27 '21 at 08:12
  • @MathLover I want to say $BP = CQ$ is obvious, but somehow I can't figure out why too. If $\triangle BPR$ and $\triangle CQR$ are congruent, then the problem is solved, but there is no angle-side-side postulate. So I wonder how would you prove it. – VTand Nov 27 '21 at 08:13
  • @JohnOmielan, That’s the thing. If we assume PQ is not parallel to BC, the diagram changes. It has to, because PQ and BC ARE parallel to each other. I wondered if I could use some sort of proof by contradiction to prove this but I’m not really sure. It’s like you don’t have enough information to write a solid proof but assuming something otherwise changes the diagram and thus the question. – Afsheen Nov 27 '21 at 08:35
  • @VTand, Exactly! I actually asked this because I came across a problem that asked me to find Angle BPR, given Angle A. And the solution required me to prove Angle APQ = Angle ABC which means PQ is parallel to BC. And though that completely makes sense, I just don’t know how. – Afsheen Nov 27 '21 at 08:45
  • 1
    @Afsheen your diagram is a bit misleading. It depends on whether it is an acute angled isosceles triangle or obtuse angled isosceles triangle. – Math Lover Nov 27 '21 at 08:52
  • @VTand my comment is for acute angled isosceles triangle – Math Lover Nov 27 '21 at 08:53
  • 1
    @MathLover Yes, with an acute angled isosceles triangle, your comment is correct. Otherwise, as my previous comment indicates, if $\measuredangle BAC = 120^{\circ}$ (i.e., is an obtuse angled isosceles triangle), then a counter-example is possible. – John Omielan Nov 27 '21 at 08:55
  • 1
    @JohnOmielan yes you are right. I did not notice that the triangle was not acute angled. I just added a diagram that shows the counter-example. – Math Lover Nov 27 '21 at 09:09

1 Answers1

5

Please see the below diagram which gives a counter-example for obtuse angled isosceles triangle ($120$-$30$-$30$) as mentioned by John Omielan.

enter image description here

For $\angle BRP = 60^\circ + x, \angle CRQ = 60^\circ - x$ or vice versa with $0 \lt x \lt 30^\circ$ will give us points $P$ and $Q$ on sides $AB$ and $AC$ such that $\triangle PQR$ is equilateral but $PQ$ is not parallel to $BC$.

By law of sines, we can show that $120$-$30$-$30$ is the only isosceles triangle for which $PQ$ is not necessarily parallel to $BC$.

Say $\angle B = \angle C = y$ and $\angle BRP = 60^\circ + x, \angle CRQ = 60^\circ - x$

By law of sines in $\triangle BPR$,

$ \displaystyle \frac{\sin (180^\circ - (60^\circ + x+y))}{BR} = \frac{\sin y}{PR} \tag1$

By law of sines in $\triangle CQR$,

$ \displaystyle \frac{\sin (180^\circ - (60^\circ - x + y))}{CR} = \frac{\sin y}{QR} \tag2$

As $BR = CR$ and $PR = QR$, from $(1)$ and $(2)$ we obtain

$\sin (60^\circ - x + y) = \sin (60^\circ + x + y)$

So we either have $60^\circ - x + y = 60^\circ + x + y ~$ i.e. $ ~x = 0$. That leads to $\angle BRP = \angle CRQ = 60^\circ ~$ and $ ~PQ \parallel BC$.

Or we have,

$(60^\circ - x + y) + (60^\circ + x + y) = 180^\circ \implies y = 30^\circ$ and $\triangle ABC$ is $120$-$30$-$30$ triangle. In this case, it is not necessary that $ \angle BRP = \angle CRQ$. I have demonstrated this case in the first part of my answer.

Math Lover
  • 52,200