Is it possible to realize the Klein bottle as a linear group orbit?

Question

Does there exists a Lie group $ G $, a finite dimensional representation $ \pi: G \to GL(V) $, and a vector $ v \in V $ such that the orbit $$ \mathcal{O}_v=\{ \pi(g)v: g\in G \} $$ is diffeomorphic to the Klein bottle?

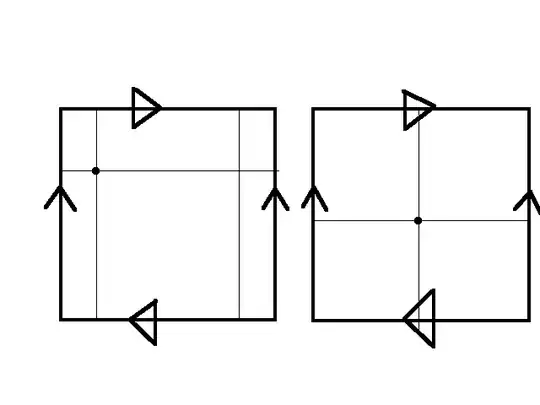
The Klein bottle, $ K $, is homogeneous for the special Euclidean group of the plane $$ SE_2= \left \{ \ \begin{bmatrix} a & b & x \\ -b & a & y \\ 0 & 0 & 1 \end{bmatrix} : a^2+b^2=1 \right \} $$ Because there is a one parameter group $ H $ of translations up each vertical line $$ H= \left \{ \ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & y \\ 0 & 0 & 1 \end{bmatrix} : y \in \mathbb{R} \right \} $$ There is also an element that shifts horizontally by one unit $$ b:=\begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$ If we mod out $ SE_2 $ by the group generated by $ \langle H,b \rangle \cong \mathbb{R} \times \mathbb{Z} $ we just get a torus. Now if we include the rotation by 180 degrees $$ r:=\begin{bmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$ Then mod out $ SE_2 $ by the group generated by $ \langle H,r,b \rangle $ we get the Klein bottle $ K $. Since $ \mathbb{Z}=\pi_1(SE_2) $ and $ \pi_0(<H,r,b>) =<r,b> \cong \{ \pm 1 \} \rtimes \mathbb{Z} $ then we must have $$ 0 \to \mathbb{Z} \to \pi(K) \to \mathbb{Z} \rtimes \{ \pm 1 \} \to 0 $$ So we can conclude that $ \pi_1(K) \cong \mathbb{Z} \rtimes (\mathbb{Z} \rtimes \{ \pm 1 \}) $. It turns out that this particular semidirect product is isomorphic to the simpler semidirect product $ \mathbb{Z} \rtimes \mathbb{Z} $ with presentation $ <a,b:abab^{-1}> $ . Thus $ \pi_1(K) \cong \mathbb{Z} \rtimes \mathbb{Z} $ (this fact can be verified using the Seifert-Van Kampen theorem and the fact that a Klein bottle is a connected sum of two projective planes)

As Steve D pointed out below, since the klein bottle has orientable double cover the torus then by applying LES of homotopy to the $C_2$ principal bundle we have $$ 1 \to \mathbb{Z}^2 \to \pi_1(KB) \to C_2 \to 1 $$ So the fundamental group is virtually abelian.

Answer 1

The answer is no.

A compact linear group orbit must have a transitive action by a compact Lie group (which is equivalent to being a compact manifold which admits a metric with respect to which it is Riemannian homogeneous) see

https://mathoverflow.net/questions/409511/compact-linear-group-orbit-equivalent-to-linear-compact-group-orbit

The klein bottle is compact and aspherical (universal cover is the plane). The only compact aspherical linear group orbit is the torus see

Riemannian homogeneous aspherical iff flat torus

Answer 2

This is an extended comment on the question - apologies for posting as answer.

Firstly I find it really interesting that you have this transitive $SE_2$ action on the Klein bottle. Naively one might think that as the Klein bottle inherits a locally Euclidean metric as a quotient of the plane by a subgroup $G\subset E_2$ (with $G\cong \pi_1(K)$), there would be such a transitive $SE_2$ action of isometries. However $G$ is not central in $E_2$ so the action of $SE_2$ as isometries is not well defined. Further if we consider pairs of geodesics parallel to the sides of a fundamental rectangle, meeting orthogonally at different points:

we see that the length of the vertical geodesic is doubled when the point does not lie in the middle vertical line.

This does not prove that $SE_2$ does not act transitively isometrically on the Klein bottle - but it is very unlikely as the points in the middle (and sides) seem to be genuinely different to the rest.

On the other hand, both here and in your comment you give beautiful transitive actions of $SE_2$ on the Klein bottle - which made me wonder what quadratic structure on the tangent bundle they might preserve.

Following the construction from your comment, parametrise the Klein bottle by $$K=\{(c,\theta)| c\in [0,1], \theta\in [0,\pi]\}/\sim,$$ with $k_1\sim k_2$ precisely when they result in the same set of lines in $\mathbb{R}^2$:$$\{(x,y\}|\,\,(\cos\theta) x+(\sin\theta) y\equiv c\mod 1\}.$$

As you said, the action of $SE_2$ on these sets of lines (induced from the natural action on $\mathbb{R}^2$), gives us an action on $K$. A bilinear form on the tangent bundle is invariant under $SE_2$ precisely when it is induced by translations, from a bilinear map at a point, invariant under the stabiliser of the point.

The stabiliser of $(0,\pi)\in K$ is precisely translations by $(0,\lambda),\lambda\in \mathbb{R}$, translations by $(n,0),\, n\in\mathbb{Z}$ and rotations by $\pi$. This is precisely your $\langle H,r,b\rangle$, so the two constructions you gave are the same (sorry - this is probably obvious to you, but I only just realised).

The action of $(0,\lambda)$ sends $(c,\theta)\mapsto (c+\lambda \cos\theta)$, so has derivative $$\left(\begin{array}{cc}1&\lambda\\0&1\end{array}\right).$$

The forms invariant under this are precisely the ones of the form: $$\left(\begin{array}{cc}0&a\\-a&b\end{array}\right).$$

So your action is not compatible with any metric. Locally though we can define an area form: $$\left(\begin{array}{cc}0&1\\-1&0\end{array}\right).$$

However the derivative of rotation by $\pi$ is: $$\left(\begin{array}{cc}-1&0\\0&1\end{array}\right),$$ so area gets flipped when you cross the boundary that reverses orientation (as one would expect).

The only bilinear form that is globally invariant under $SE_2$ is then (up to scalar): $$\left(\begin{array}{cc}0&0\\0&1\end{array}\right).$$

We do not need to worry about translations by $(n,0)$ as these have derivative the identity.

Apologies for rambling, but I found this action you described (two different ways) very interesting.