Let $$\begin{align} a_0 &=0, & a_1&=1, & a_{n+1}+a_{n-1}&=\frac{8a_n}{16-5a_n^2}\end{align}$$
Show that $$a_{2n}^2 = \frac{64(5a_n^4-20a_n^2+16)a_n^2}{(5a_n^4-16)^2}$$
My thoughts so far:
Since $a_n$ is rational number, it implies that $5a_n^4-20a_n^2+16$ is square of another rational number so that it should be related to curve $y^2=5x^4-20x^2+16$? (In another link it shows how to transform it into elliptic curve.)
For example $\displaystyle a_2=\frac8{11}, a_3=-\frac{57}{101},a_4=-\frac{13904}{13361}$
? f(a0,a1)=8*a1/(16-5*a1^2)-a0
%50 = (a0,a1)->8*a1/(16-5*a1^2)-a0
? f(0,1)
%51 = 8/11
? a2=f(0,a1)
%52 = 8/11
? a3=f(a1,a2)
%53 = -57/101
? a4=f(a2,a3)
%54 = -13904/13361
? a5=f(a3,a4)
%55 = -259735/1169341
? a6=f(a4,a5)
%56 = 1495852824/1612186411
? g(x)=64*(5*x^4-20*x^2+16)*x^2/(5*x^4-16)^2
%57 = (x)->64*(5*x^4-20*x^2+16)*x^2/(5*x^4-16)^2
? g(a3)-a6^2
%58 = 0
? g(a3)
%59 = 2237575671068774976/2599145023813060921
? a6^2
%60 = 2237575671068774976/2599145023813060921
? g(a2)-a4^2
%61 = 0
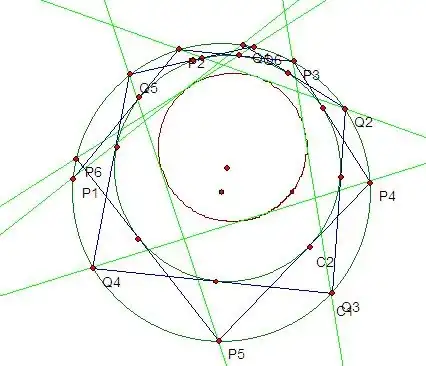
The geometry background of the problem
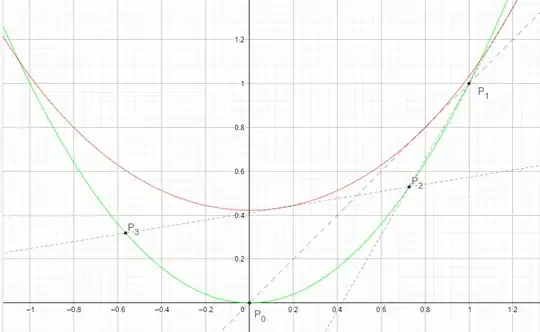
Let curve $C_0: y=x^2$ and $C_1: 4x^2+y^2-8y+\frac{16}5=0$,
Point $P_0(0,0)$ is in curve $C_0$.
From point $P_0$ we could find two tangent line of $C_1$ and one of them intersect $C_0$ at $P_1(1,1)$.
From point $P_n(a_n, b_n)$, we could find a tangent line of $C_1$ not passing through $P_{n-1}$ which intersect $C_0$ at $P_{n+1}(a_{n+1},b_{n+1})$.
As an extension of Poncelet's Theorem, I have found that lines $P_0P_k, P_1P_{k+1},P_2P_{k+2},...,P_hP_{k+h},...$ are all tangent to a conic section $C_{t_k}$ and $C_{t_k}$ passing through the intersection of $C_0$ and $C_1$ so that we could write $C_{t_k} = C_0 + t_k C_1$.
And more general, similar to list $P_0,P_1,P_2,...$, starting from another point $Q_0$ in $C_0$, we could form another list $Q_0, Q_1,Q_2,...$, then lines $P_0Q_0, P_1Q_1,P_2Q_2,...$ are all tangent to a conic section passing through the intersection of $C_0$ and $C_1$.
We could always using a $3\times 3$ matrix to represent a conic section in homogenous coordinates so that $\begin{bmatrix}A&B&C\\B&D&E\\C&E&F\end{bmatrix}$ could be used to represent the curve $Ax^2+2Bxy+Dy^2+2Cx+2Ey+F=0$.
So $C_0=\begin{bmatrix}1&0&0\\0&0&-\frac12\\0&-\frac12&0\end{bmatrix}$ and $C_t=\begin{bmatrix}1+3t&0&0\\0&t&-\frac{1+7t}2\\0&-\frac{1+7t}2&\frac{16t}5\end{bmatrix}$.
$C_t^{-1}=-\frac{1}{181t^2+70t+5}\begin{bmatrix}\frac{-181t^2 - 70t - 5}{3t + 1}&0&0\\0&64t&70t+10\\0&70t+10&20t\end{bmatrix}$
Next, if there're two points $(x_1,x_1^2), (x_2,x_2^2)$ in $C_0$ and the line through them is tangent to $C_t$, we could find that $\begin{pmatrix}-(x_1+x_2)&1&x_1x_2\end{pmatrix}C_t^{-1}\begin{pmatrix}-(x_1+x_2)\\1\\x_1x_2\end{pmatrix}=0$. According to definition of $C_{t_k}$, There're points $(x_1,x_1^2),(x_2,x_2^2),(x_3,x_3^2)$ so that
$\begin{cases}\begin{pmatrix}-(x_1+x_2)&1&x_1x_2\end{pmatrix}C_{t_k}^{-1}\begin{pmatrix}-(x_1+x_2)\\1\\x_1x_2\end{pmatrix}=0\\
\begin{pmatrix}-(x_2+x_3)&1&x_2x_3\end{pmatrix}C_{t_k}^{-1}\begin{pmatrix}-(x_2+x_3)\\1\\x_2x_3\end{pmatrix}=0 \\
\begin{pmatrix}-(x_1+x_3)&1&x_1x_3\end{pmatrix}C_{t_{2k}}^{-1}\begin{pmatrix}-(x_1+x_3)\\1\\x_1x_3\end{pmatrix}=0
\end{cases}$
Let $x_2=0$ we get quadratic equations of $x_1,x_3$ with same coefficients (in parameter $t_k$). By Vieta's formulas, from the first two equations, we have $x_1x_3=-r(t_k)=-\frac{192t_k^2+64t_k}{181t_k^2+70t_k+5}$ and $t_{2k}=\frac{5r(t_k)}{5r(t_k)^2-35r(t_k)+16}$.
Now let $x_1=a_0=0$, and substituted into 3rd equation and we have $a_{2k}^2 = r(t_{2k})$ and similar we have $a_k^2=r(t_k)$ and finally we could get the relationship between $a_k^2$ and $a_{2k}^2$.
Similarly by composite $C_1$ and $C_k$ and applying Vieta's formula, we have $a_{k-1}+a_{k+1}=\frac{8a_k}{-5a_k^2+16}$ to verify the recursive formula in the problem is held for the sequence.
Relationship with Elliptic curve
Let $K_h=h(x^2-y)+(4x^2+y^2-8y+\frac{16}5)$
The characteristic polynomial of matrix $f(x)=C_0^{-1}C_1$ is $x^3-20x+\frac{576}5x-\frac{1024}5$
Define elliptic curve $y^2=-f(0)f(-x)=\frac{1024}5(x^3+20x+\frac{576}5x+\frac{1024}5)$
And point $A_1=(0,-f(0))$ is a point in the elliptic curve.
Let $A_n = [n]A_1 =(x_n,y_n)$ in the elliptic curve group, the $K_{x_n}$ represent same curve as $C_{t_n}$.
