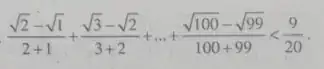Proving $\sum_{n=1}^{99}\frac{\sqrt{n+1}-\sqrt{n}}{2n+1}\lt\frac9{20}$

Question

I found the original question asked by someone else, asking for this to be proven using only '9th grade math', this is the image:

Which can be written like

$$\sum_{n=1}^{99}\frac{\sqrt{n+1}-\sqrt{n}}{2n+1}\lt\frac9{20}$$ Rationalizing it, I got

$$\sum_{n=1}^{99}\frac{1}{(2n+1)(\sqrt{n+1}+\sqrt{n})}<\frac9{20}$$

This is where I'm stuck. My plan was to somehow turn this into a telescoping sum, but I had no luck with that because of how messy the denominator can get in partial sums. I've tried to see if it followed the pattern of a GM series but the resulting ratio had radicals in. I generally don't know how to do sums of radicals. So how can I prove this inequality, preferably without using induction or manually evaluating each term using a calculator (because of the 9th grade math condition)? Any help is appreciated.

Answer 1

As we know $(2n+1)^2=4n^2+4n+1>4n^2+4n=4n(n+1)$, then $2n+1>2\sqrt{n(n+1)}$, with $n\in\mathbb N$. Hence we have $$ \sum_{n=1}^{99}\frac{\sqrt{n+1}-\sqrt{n}}{\color{red}{2n+1}}<\sum_{n=1}^{99}\frac{\sqrt{n+1}-\sqrt{n}}{\color{red}{2\sqrt{n(n+1)}}}=\frac{1}{2}\sum_{n=1}^{99}\frac{1}{\sqrt n}-\frac{1}{\sqrt{n+1}}=\frac{1}{2}\left(1-\frac{1}{10}\right)=\frac{9}{20}. $$