2

I'm trying to find a nice similarity between e and pi and I thought of conic sections. If you have a circle then the perpendicular conic section to that is a hyperbola. So this seems pretty similar. I thought i can probably use this. But now i'm trying to get e in a similar way out of it

I know its in the hyperbolic functions, but I can't find a nice analogy for pi and the ratio of perimeter and diameter (how would you find that for a hyperbolic curve?). I thought of the integral of a hyperbolic function which is natural logarithm but it didn't really work.

Or is there a projective geometrical way of thinking it?

Hopefully someone can help me! I'm strongly convinced that there must be an easy/simple way of finding this analogy, especially because the hyperbola <> circle analogy

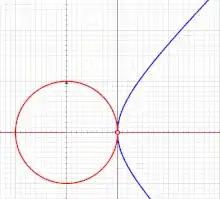
EDIT: I don't know anything about projective geometry, but if you look at this picture https://fractad.files.wordpress.com/2011/02/hyperbola-plot.jpg

Then it seems that the circumference of the circle becomes the arc length of the hyperbola and the diameter becomes just the whole domain x. Would it then work if you do:

arc length hyperbola/ arc length domain? That would be something like:

$ L_{hyperbola} = \int \sqrt {1+1/x^4 } dx $

$ L_{domain} = x$

$ L_{hyperbola}/L_{domain} = $

But then I get an ugly equation so this probably doesn't make sense:

$ 1/x \int \sqrt{(1 + 1/x^4)} dx = (1/x) (constant -(\sqrt{(1/x^4 + 1)} x_2 F_1(-1/2, -1/4, 3/4, -x^4))/ \sqrt{(x^4 + 1)}) $

Parcly Taxel
  • 105,904
bananenheld
  • 629
  • Both hyperbolic and trigonometric functions are built using the powers of $e$, but trigonometric functions add an imaginary factor to the formulas. Eg. $cos(x) = \frac{e^{ix}+ e^{-ix}}{2}$ $cosh(x) = \frac{e^{x}+ e^{-x}}{2}$ . The constant $\pi$ appears because of the periodicity of the trigonometric side of things, $(e^{i2\pi} = 1)$ which is notably absent in the hyperbolic case. So the similarity linking hyperbolic to trigonometric is between $1$ and $i$, with powers of $e$ acting as a building block for both. $\pi$ seems secondary. – user3257842 Nov 05 '21 at 09:44
  • See https://docplayer.net/52861430-Through-the-looking-glass-a-glimpse-of-euclid-s-twin-geometry-the-minkowski-geometry.html – user3257842 Nov 05 '21 at 09:45
  • $e^{it}$ has the period $2\pi$, while $e^t$ is aperiodic. It could be that the similarity stops here. And contrary to the circle, the hyperbola does not have a closed-form expression for its length. – Bobby Laspy Nov 05 '21 at 11:00
  • There's a conjecture that $e$ is not a period, while $\pi$ is. – Jan-Magnus Økland Nov 05 '21 at 11:13
  • If it helps, I like this answer to another question which explicitly shows segments of length $e^u$ and $e^{-u}$ on the plot: https://math.stackexchange.com/a/757241/441161 – Andy Walls Nov 06 '21 at 13:28

2 Answers2

3

There is no analogy between the constants. They play totally different roles.

On the other hand, you can draw a lose analogy between $\pi$ and Euler-Mascheroni constant $\gamma$ because the regularized value of the integral $\int_0^\infty \frac1x dx$ is $\gamma$. So, it is a regularized value of the "area" under hyperbola.

One also can notice that the area of the hyperbolic sector between the unit hyperbola $y=\sqrt{x^2-1}$ and the diagonal $y=x$ regularizes to $\gamma/2$ (when integrated in polar coordinates), but we know that twice the area of the hyperbolic sector corresponds to hyperbolic angle. So, does $\gamma$ corresponds to infinite hyperbolic angle.

https://upload.wikimedia.org/wikipedia/commons/8/8a/HyperbolicAnimation.gif

In many formulas there is also an analogy between $\pi/4$ and $e^{-\gamma}$.

Anixx
  • 10,161
  • $\gamma$ also is conjectured not to be a period. – Jan-Magnus Økland Nov 05 '21 at 11:26
  • @Jan-MagnusØkland yes, I am pretty sure, it is not a period, but if we generalize the concept of periods to divergent integrals, then $\int_0^1\frac1x dx$ would be a period (by definition), and its regularized value is $\gamma$. So, $\gamma$ is a finite part of what we could call a "generalized period" – Anixx Nov 05 '21 at 11:27
2

This is an interesting question, but I don't think it has the kind of answer you are looking for. If you move from affine to projective co-ordinates there is essentially only one kind of conic. The fact that the rectangular hyperbola (which would be a more accurate counterpart to the circle than the general hyperbola) allows you to recover the natural logarithm through the integral (ie area) gives some kind of analogy is remarkable in itself - I am not sure what more you would want.

There is a link between the ellipse and the hyperbola in that the ellipse can be parametrised using the functions sine and cosine, while the equivalent parametrisation of the hyperbola uses the equivalent hyperbolic functions. But that has more to do with complex numbers and the function of $i=\sqrt {-1}$ in the equations than $e$ or $\pi$.

Of course the formula $e^{i\pi}=-1$ lurks in the background, but with $\pi$ as the exponent here, getting $e$ and $\pi$ into some kind of equivalence suggests the use of logarithms.

Mark Bennet
  • 101,769