I am trying to find a solution to the following integral. $$ \int \sqrt {17+8\cos(3t)+9\cos^2(3t)} dt$$
I have run into exactly the same problem as this previous unanswered question. This integral appears when you try and find the arclength of the Trefoil knot. The previous author found an equation where $\theta$ was put in terms of $t$. But it was not possible to invert it, and like the author I would like a function where $t$ is put in terms of $\theta$.
I have looked at Gradshteyn and Rhyzik's Tables of Integrals, Series and Products. And in the seventh edition, integral 2.580 - 2 appears to be similar. It has the following form.
$$ \int \frac{dt}{\sqrt {a+b\cos(t)+c\sin(t) + d\cos^2(t) + e\sin(t)\cos(t)+f\sin^2(t)}} $$
The book states if I undertake the following substitutions, let $x = tan(t/2)$, $A=a+b+d$, $B = 2c+2e$, $C=2a-2d+4f$,$D=2c-2e$,$E=a-b+d$, then it is equivalent to the integral below. $$2\int \frac{dt}{\sqrt{A+Bx+Cx^2-Dx^3+Ex^4}}$$
Its not that hard to put my trigonometric polynomial into a similar form, one obtains the following result.
$$\sqrt{34+16x^2+18x^4}$$
However I never covered elliptic integrals and I have no idea if it's a viable solution to the problem I have. Obviously the immediate difference is that I have an integral that is not an inverse like the elliptic form I found. Is there a trick I can use to make my integral into that form? Or is this path a dead end? Any clarification or help would be much appreciated.
UPDATE I've managed to cobble together a different attack on this problem, but I still do not have a solution. Critical details were found in a number of engineering papers describing applications of knots to antennas, one of which is cited below. All were by the same author and covered similar ground.
The author was investigating (p,q) Elliptical Torus knots. They have the following parametrization. $$ x = (a + bcos(\psi + qs))cos(ps)$$ $$ y = (a + bcos(\psi + qs))sin(ps)$$ $$ z = csin(\psi+qs)$$ Where $0\leq s \leq2\pi$ and $a$ and $b$ are arbitrary parameters. The (2,3) Torus Knot is a Trefoil, and if we let $ c= b$ then we have a circular trefoil torus knot. The author states but does not derive the following formula for the arc length of this class of knots. $$ L_{pq}= 2\int_{0}^{2\pi} \sqrt{p^2(a+b cos(u))^2+q^2(b^2sin^2(u)+c^2cos^2(u))}du$$ If we apply the the parameters noted above, the following definite integral appears.
$$ L_{23}= 2\int_{0}^{2\pi} \sqrt{2^2(a+b cos(u))^2+3^2(b^2sin^2(u)+b^2cos^2(u))}du$$
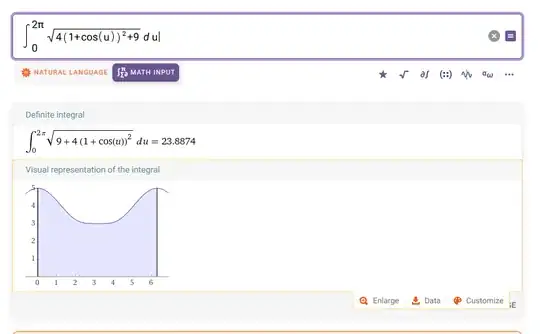
And via a basic trig identity simplifies to the following. $$ L_{23}= 2\int_{0}^{2\pi} \sqrt{4(a+b cos(u))^2+9b^2}du$$
So I have a definite integral. I can numerically integrate this version, and I obtain the answer below if I let a=b=1. It would still be nice to have an analytic solution though!
Werner, Douglas H.; Jones, D. M.; Werner, P. L., The electromagnetic fields of elliptical torus knots, IEEE Trans. Antennas Propag. 49, No. 6, 980-991 (2001). ZBL1368.78029..