Why does Green's function depend on contour?

Question

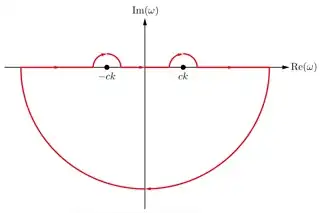
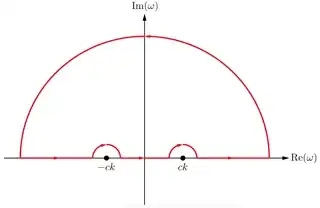
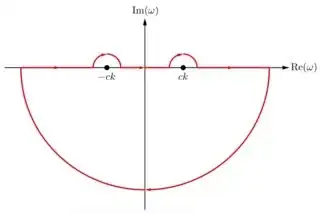
I am trying to find a Green's function for the wave equation: \begin{equation} \bigg(\nabla^2 - \frac{1}{c}^2\frac{\partial^2}{\partial t^2}\bigg)G(\textbf{r},t) = \delta^3(\textbf{r})\delta(t) \end{equation} After a fairly trivial calculation, one easily finds that \begin{equation} G(\textbf{r},t) = \frac{1}{4\pi^3} \int_0^\infty dk \ c^2 k^2 \frac{\sin(kr)}{kr} \int_{-\infty}^\infty d\omega \frac{e^{-i\omega t}}{(\omega-ck)(\omega+ck)} \end{equation} I am mainly interested in the integral in $\omega$: \begin{equation} \int_{-\infty}^\infty d\omega \frac{e^{-i\omega t}}{(\omega-ck)(\omega+ck)} \end{equation} We can evaluate this integral in the complex $\omega$-plane by choosing a contour running over $\text{Re}(\omega)$ but jumping over the poles at $\omega=\pm ck$. There are several choices for such a contour, and I'm wondering why choosing one contour will give a different value for this integral than another?

For example, suppose that $t<0$ so that $e^{-i \omega t} \rightarrow 0$ as $\omega\rightarrow i\infty$. This suggests that we close our contour in the upper half plane ensuring that the integral due to the upper semi-circle does not give any contribution. This contour does not enclose either pole so by the residue theorem the integral vanishes.

Now consider $t>0$. Then $e^{-i\omega t} \rightarrow 0$ as $\omega \rightarrow -i\infty$. This suggests that we close our contour in the lower half plane ensuring that the integral due t the lower semi-circle doe snot give any contribution. This time, we enclose both poles, so by the residue theorem: \begin{equation} \int_{-\infty}^\infty d\omega \frac{e^{-i\omega t}}{(\omega-ck)(\omega+ck)} = -2\pi i\bigg(\frac{e^{-ickt}}{2ck}-\frac{e^{ickt}}{2ck}\bigg) = -\frac{2\pi}{ck} \sin (kct), \ t>0 \end{equation} where the negative sign comes from the fact that the contour runs clockwise. This gives rise to a retarded Green's function.

However suppose that instead of skipping over the poles I not skip under them. The integral now evaluates to something else (which gives an advanced green's function): \begin{equation} \int_{-\infty}^\infty d\omega \frac{e^{-i\omega t}}{(\omega-ck)(\omega+ck)} = 2\pi i\bigg(\frac{e^{-ickt}}{2ck}-\frac{e^{ickt}}{2ck}\bigg) = \frac{2\pi}{ck} \sin (kct), \ t<0 \end{equation} So which of these contours am I to choose? Why do they give different values for a definite integral?

Answer 1

Summary of comments: The integral diverges because of the non-integrable poles on the integration contour. Since these poles are of first order, the Cauchy principle value (PV) of the integral exists, and corresponds to avoiding the poles with semi-circular arcs. The PV is unchanged whether we make an arc above or below the pole. This is a type of regularization. Other regularizations may give different results. Even though we will be integrating above/ below the poles, this is different to the popular $\pm i \epsilon$ prescription whereby one considers a related integrand with poles shifted above or below the axis$^\dagger$ (the $\pm i\epsilon $ regularization leads to results that do depend on the contour taken).

The principle value is

$$\tag{1} \text{PV}\int_{-\infty}^\infty d\omega \frac{ e^{-i\omega t}}{\omega^2-k^2} = -\frac{\pi}{k}\sin(k|t|) $$

Consider the case $t>0$, so we close the contour in the lower half plane. I've also set $c=1$ for my convenience. Suppose we make arcs above the poles:

Then we have by residue theorem

$$\tag{2} I+C_-+C_++C_R=-2\pi i (R_- +R_+) $$

Where $I$ is the integral in eq (1), $C_{\pm}$ are the contributions due to integrating over the poles at $\pm k$, $C_R$ is the (vanishing) contribution due to the large arc, $R_\pm$ are the residues at $\pm k$, and the minus sign on the RHS is because the contour is CW.

Near the pole $\omega=k$ we can write

$$ \frac{ e^{-i\omega t}}{\omega^2-k^2} = \frac{e^{-ikt}}{2k(\omega-k)} + \text{finite} $$

To integrate around the pole, parameterize: $\omega=k+\epsilon e^{i\phi}$, then $d\omega=i \epsilon e^{i\phi}d\phi$. Integrating around a CCW semicircle yields

$$\tag{3} \int\limits_0^\pi \frac{i e^{-ikt}}{2k} d\phi + \mathcal{O}(\epsilon) = i\pi \left(\frac{ e^{-ikt}}{2k}\right) + \mathcal{O}(\epsilon) $$

When we take the radius of the arc, $\epsilon$ to zero, all the other terms vanish. The result is precisely $i\pi$ times the residue at the pole. This will generally be the case for simple first order poles$^\ddagger$. Substituting this and the similar calculation for the other pole into eq (2) we have

$$ I-i\pi R_- - i \pi R_+ = -2 \pi i (R_-+R_+) $$

The new minus signs on the LHS are because of the orientation of $C_\pm$. We are left with

$$ I=-i\pi(R_-+R_+)=-i\pi \left(-\frac{e^{ikt}}{2k}+\frac{e^{-ikt}}{2k} \right)=-\frac{\pi}{k}\sin(kt) $$

Suppose we instead made the arcs beneath the poles (still with $t>0$). The analogue of eq (2) is

$$ I+C'_-+C'_+=0 $$

Where $C'_\pm$ are the contributions due to CCW arcs beneath the poles (already calculated in eq (3), they differ only by a sign from the $C_\pm$). The RHS is zero as this contour encloses no poles. Substituting in

$$ I+i\pi R_-+i\pi R_+=0 \\ I=-i \pi (R_- + R_+) $$

Precisely as before. You can check that other combinations of above/ below the poles yield the same result. When $t>0$, the solution will be (slightly) different, but using the same method you can show that the answer is independent of whether your chosen contour goes above or below the poles.

$\dagger$ A fact that even some well respected textbooks forget.

$\ddagger$ You can see why this only works for first order poles, if there were any terms more singular than $1/\omega$ in eq (3), there would remain contributions proportional to $1/\epsilon$ which prevent the limit of zero radius being taken safely.