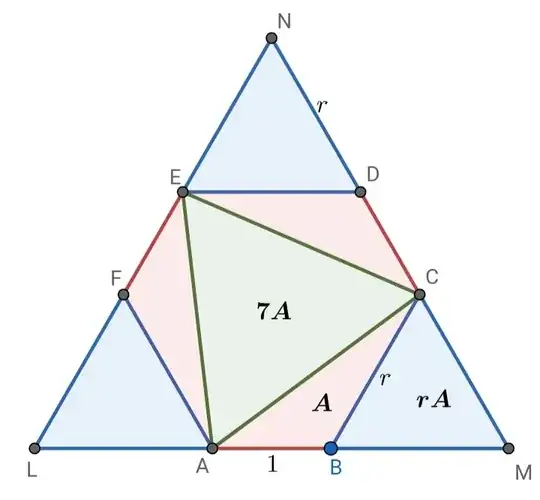
Equiangular hexagon $ABCDEF$ has side lengths $AB=CD=EF=1$ and $BC=DE=FA=r$. The area of $\triangle ACE$ is $70\%$ of the area of the hexagon. What is the sum of all possible values of $r$? AMC 10A 2019#17, AMC 12A 2010#17
Since this was asked in AMC 12, Law of Cosines is an appropriate tool. And the video solution at the link above does it beautifully. However, since it was asked in AMC 10 as well, there (usually) should be a non-trig solution as well.
Can anyone help with a geometrical solution? (Note: I understood the trig solution, but can't think of a geometrical solution).