Disclaimer: I have posted this question on mathoverflow.net following the instructions of this topic.
If we take two apparently simple first order ODE's like $y'=y$ and $y'=y^2$ we find that:
For the first one the general solution is $y=C\exp(t)$ and is defined for all $t$.
For the second one, the general solution is $y=\frac{1}{C-t}$ and it's defined only for $t<C$.
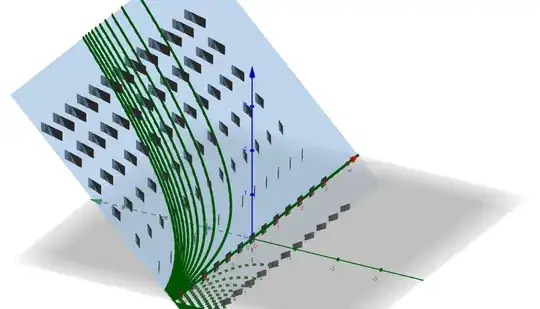
There is a way to 'see' geometrically the solutions of these equations as leaves of the "Characteristic Foliation" of the standard contact structure of $R^3$. Look at this site and this article for some nice pictured examples.
Looking for the characteristic foliation of the two equations, the shape of the surface seens to play a big role. Apparently is the curvature of the surface that, somehow, 'controls' the growth of solutions.
My question is: Are there some notion of curvature that explains why nonlinear EDO's can have solutions with movable singularities?
I know that Contact geometry doesn't have local invariants as Riemannian geometry, so, I believe, the answer to this question lies beyond the domain of Contact/Symplectic geometry.
ps: taking other linear and nonlinear equations, with or without time varying coeficients, I had the same impression.
Here are some pictures that I made:
Characteristic foliation for $y'=y$
Characteristic foliation for $y'=y^2$
