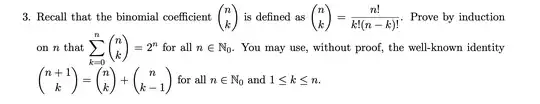I did prove the base case where n=0. Now I was trying to prove the induction step(n+1).
I tried doing: $$2^{1+n} = 2^{n} + \sum \binom{n+1}{k}$$ $$2^{1+n} = 2^{n} + \sum \binom{n}{k} + \sum \binom{n}{k-1}$$ $$2^{1+n} = 2^{n} + 2^{n} + \frac{n!}{\left ( k-1 \right )!\left ( n-k-1 \right )!}$$
I tried cancelling the last part of the equation, but it doesn't work. Could someone explain and show me the way.