How to compute $\int_{-\infty}^{\infty} \exp(i \pi x^2) dx$?

Question

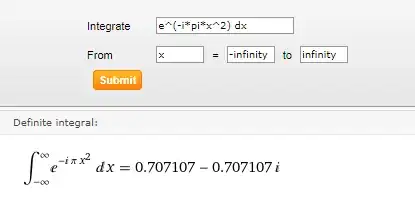
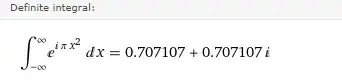
I want to compute something similar to the Gaussian integral like below: \begin{align} I = \int_{-\infty}^{\infty} \ e^{(i\pi x^2)}dx \end{align} WolframAlpha says the result is $I = \sqrt{i}$ but I have no idea how to get this answer. Below is the derivation I tried: \begin{align} I^2 &= \left(\int_{-\infty}^{\infty} e^{(i\pi x^2)}dx \right) \left(\int_{-\infty}^{\infty} e^{(i\pi y^2)}dy \right)\\ &= \int_{-\infty}^{\infty} e^{\{i\pi (x^2+y^2)\}}dx \end{align} Let $x = r \cos{\theta}, \ y = r \sin{\theta}$, then \begin{align} I^2 &= \int_{0}^{2\pi}\int_{0}^{\infty} e^{(i\pi r^2) } r \ dr \ d\theta \\ &= 2 \pi \int_{0}^{\infty} e^{(i\pi r^2) } r \ dr \end{align} Let $s=r^2$, then $ds = 2r dr$. Thus, \begin{align} I^2 &= 2\pi\int_0^{\infty}e^{(i\pi r^2)}\cdot\frac{1}{2}\cdot 2rdr \\ &= \pi \int_0^{\infty}e^{(i\pi s)}ds \\ &= \frac{1}{i} e^{(i\pi s)}|_{0}^{\infty} \end{align} Here, I get a problem. I tried to compute the limit: $$\displaystyle{\lim_{s\rightarrow\infty}} e^{(i\pi s)} = \displaystyle{\lim_{s\rightarrow\infty}} \cos{(\pi s)} + i \sin{(\pi s)}$$ but I think it becomes indeterminate.

Am I doing something wrong? How do you get $I=\sqrt{i}$ ?

Essentially all methods boil down to computing $$\lim_{a\to0^+}\int_{-\infty}^\infty \exp(-(a-i)\pi x^2):dx$$ to varying levels of rigor. Pick the level you're happiest with. — Ninad Munshi, Sep 26 '21 at 15:27
one of the solutions is here https://math.stackexchange.com/questions/3999803/complex-gaussian-integral-by-change-of-variable/4000082#4000082 — Svyatoslav, Sep 26 '21 at 15:37
Hang on a minute $\int_{-\infty}^{\infty}exp(i\pi x^{2})dx$ is clearly divergent. If it is $\int_{-\infty}^{\infty}exp(-i\pi x^{2})dx$ . Then it is convergent. — Mr. Gandalf Sauron, Sep 26 '21 at 20:28

Ricardo770 · Accepted Answer · 2021-09-26T16:41:55.673

$$\begin{aligned} I &= \int_{-\infty}^{\infty} \ e^{-i\pi x^2}dx\\ &= \frac{1}{\sqrt{\pi}}\int_{-\infty}^{\infty} \ e^{-ix^2}dx\\ &= \frac{2}{\sqrt{\pi}}\int_{0}^{\infty} \ e^{-ix^2}dx\\ &= \frac{2}{\sqrt{\pi}}\left(\int_{0}^{\infty} \cos(x^2)dx-\int_{0}^{\infty} \sin(x^2)dx\right)\\ \end{aligned} $$

Consider now a more general case, namely

$$ I=\int_{0}^{\infty} e^{-i x^{a}} d x $$

let $x^{a}=t \Rightarrow x=t^{1 / a}$

$$ I=\frac{1}{a} \int_{0}^{\infty} e^{-i t} t^{1 / a-1} d t $$

Consider the following integral

$$ \int_{0}^{\infty} e^{-s t} t^{x-1} d t=\frac{\Gamma(x)}{s^{x}} $$

letting $s=i$ and $x=1 / a$ in (1) we get

$$ I=\frac{1}{a} \int_{0}^{\infty} e^{i t} t^{1 / a-1} d t=\frac{1}{a} \frac{\Gamma\left(\frac{1}{a}\right)}{i^{1 / a}}=e^{-\frac{i \pi}{2 a}} \frac{1}{a} \Gamma\left(\frac{1}{a}\right)=e^{-\frac{i \pi}{2 a}} \Gamma\left(\frac{1}{a}+1\right) $$

$$ \int_{0}^{\infty} e^{i x^{a}} d x=\int_{0}^{\infty}\left(\cos x^{a}-i \sin x^{a}\right) d x=\left(\cos \left(\frac{\pi}{2 a}\right)-i \sin \left(\frac{\pi}{2 a}\right)\right) \Gamma\left(\frac{1}{a}+1\right) \tag{1} $$

Letting $a = 2$ in $(1)$ we obtain

$$ \begin{aligned} \int_{-\infty}^{\infty} \ e^{-i\pi x^2}dx&=\frac{2}{\sqrt{\pi}}\Gamma\left(\frac{3}{2}\right)\left(\cos \left(\frac{\pi}{4}\right)-i \sin \left(\frac{\pi}{4}\right)\right)\\ &=\frac{2}{\sqrt{\pi}}\frac{\sqrt{\pi}}{2}\left(\frac{\sqrt{2}}{2}-i \frac{\sqrt{2}}{2}\right)\\ &=\left(\frac{\sqrt{2}}{2}-i \frac{\sqrt{2}}{2}\right) \qquad \blacksquare\\ \end{aligned} $$

Which agrees with Wolfram´s solution

Edit

Just noted that in your integral the exponent in the integrand is positive instead of the negative I solved for. Nevertheless this procedure is still valid and leads to the complex conjugate of my answer, which also agrees with Wolfram:

Also try $$\frac{1-i}{\sqrt 2}=\frac{1-i}{P }$$ where P is the pythagorus constant for fun. — Тyma Gaidash, Sep 26 '21 at 18:25

How to compute $\int_{-\infty}^{\infty} \exp(i \pi x^2) dx$?

1 Answers1