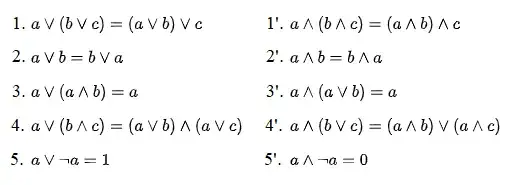It depends exactly what you mean by theory in this context.
One crucial observation is that each of the sentences you've written down is an equation - that is, the universal closure of an expression of the form "$t=s$." Now equations are preserved by Cartesian products, so for example every equation which holds in the two-element Boolean algebra ${\bf 2}$ also holds in the four-element Boolean algebra ${\bf 4}$. Consequently the sentences you've written down do not entail (for example) the sentence $$\forall x,y,z(x=y\vee y=z\vee z=x),$$ which is true in ${\bf 2}$ but false in ${\bf 4}$. Another example of such a sentence would be $$\forall x(x=0\vee x=1).$$
(I'm not sure that this "bolded number" notation is standard, but it is fairly common. In general, when it's clear from context that we're talking about structures in some class $\mathcal{K}$ where there is at most one structure up to isomorphism of each finite size, the notation "${\bf n}$" for $n\in\mathbb{N}$ is often used to refer to the isomorphism type of that unique structure. E.g. if we're talking about linear orderings, you may see "${\bf 2}$" used to denote the linear order with two elements, and so forth. I've also seen things like "$\mathbb{B}_2$" used to denote the unique-up-to-isomorphism Boolean algebra with two elements.)
This means that if we read "theory" as "first-order theory," your question has a negative answer. However, if we look at weaker logics than first-order logic, things change substantially: in fact that set of equations does generate the entire equational theory of ${\bf 2}$, that is, the set of all equations true in ${\bf 2}$. Equational logic is a very small fragment of first-order logic, and is studied in universal algebra.
I recommend Bergman's freely-available-online book as an introduction to universal algebra and equational logic; for (first-order) model theory, see the discussion here.
While not directly relevant to your question, let me as a coda present the first serious theorem in equational logic/universal algebra. Above I mentioned that Cartesian products preserve equations; it's easy to show that so do homomorphisms and substructures. These three facts provide useful tools for establishing negative results about expressibility/axiomatizability in equational logic.
However, we may now ask for a positive result: given an algebra $\mathcal{A}$, what is the set of all algebras satisfying the full equational theory of $\mathcal{A}$? This is called the variety generated by $\mathcal{A}$, and denoted "$\mathsf{Var}(\mathcal{A})$." The above paragraph gives a lower bound on $\mathsf{Var}(\mathcal{A})$: letting $\mathbb{H}$,$\mathbb{S}$,$\mathbb{P}$ be the operations on classes of structures defined by
$\mathbb{H}(\mathfrak{X})$ = the set of all homomorphic images of algebras in $\mathfrak{X}$,
$\mathbb{S}(\mathfrak{X})$ = the set of all substructures of algebras in $\mathfrak{X}$, and
$\mathbb{P}(\mathfrak{X})$ = the set of all Cartesian products of algebras in $\mathfrak{X}$,
we have $\mathsf{Var}(\mathcal{A})\supseteq\mathbb{H}(\mathbb{S}(\mathbb{P}(\{\mathcal{A}\})))$ (or "$\mathsf{Var}(\mathcal{A})\supseteq\mathbb{HSP}(\mathcal{A})$" adopting minor abuse of notation).
It turns out that this is sharp! This is Birkhoff's HSP theorem; there are several questions on this site discussing it, and I've sketched a proof here.
(As a coda to my coda, there is a similar result for first-order logic, but the algebraic operations involved are more complicated: the class of structures with the same first-order theory as a given structure $\mathcal{A}$ is the smallest class of structures containing $\mathcal{A}$ and closed under ultraproducts and ultraroots. This is somewhere in Chang/Keisler if I recall correctly, but that's a big book and I can't find it at the moment so instead see Fact $3.2.5$ here.)