I want to understand Householder transformation. I get some geometric intuition from one M.SE answer (below).
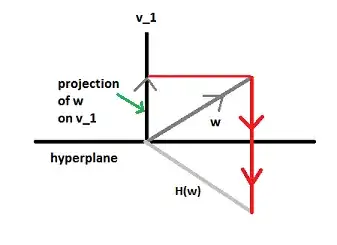
We start with a square matrix $M$ of dimension $n$. We can think of its $n$ columns as vectors in $\mathbb{R}^n$. We consider the hyperplane generated by the first column (for example the orthogonal complement of that vector). Next, we reflect each of the columns about this hyperplane. In symbols: $H_1M= [ H_1(v_1) \ldots H_1(v_n)]$, where on the RHS we use functional notation for $H_1$. Now, because $v_1$ is normal to the hyperplane, $H_1(v_1)$ looks simple. The rest of the vectors transform like:
That is we subtract twice their projections onto $v_1$ (this gives me the formula for householder reflections). Then we consider the $n-1$ dimensional submatrix of $H_1M:=M_2$, and repeat. The submatrix takes me into the hyperplane, since the first reflection leaves that plane invariant. What we are doing is changing the basis (since Reflections have $det \neq 0$) of the underlying space progressively so that the vectors have a nice representation (Thats what QR decomposition is, The Q contains the orthonormal vectors, while the R tracks all the changes we have made).
I don't understand the bolded lines.
- Like how "reflect of the columns about this hyperplane" related with tridiagonalization?
- "That is we subtract twice their projections onto $v_1$" what is mean? And how it gives us the formula for householder reflections?
In short, I want to understand the relation between the geometrical intuition with derivation of the formula.