$$x(x^2 + y^2) = a(x^2 - y^2)$$
I was trying to find the equation of the tangent as $$(Y-0) = \frac{dy}{dx}(X - 0)$$ where $$\frac{dy}{dx} = \frac{2ax-3x^2-y^2}{2(x+a)y}$$ So here putting the values of $(x,y)$ as $(0,0)$ makes the derivative non existent. I am stuck at this point and unable to proceed further.
The equation can be written as $$x(x^2 + y^2)- a(x^2 - y^2)=0.$$ It is the equation of an algebraic curve passing through the origin. It is known that the set of tangents to an algebraic curve at the origin is given by the homogeneous part of lowest total degree in the equation. Therefore, this curve has $2$ branches through the origin if $a\ne 0$, and the (global) equation of the tangents to each of these branches at the origin is $$x^2-y^2=(x-y)(x+y)=0. $$
Alternatively, when expressed in polar form, the curve is
$$r\cos\theta=a\cos2\theta$$
The tangent(s) at the pole are given by values of $\theta$ as $r\rightarrow0$
Therefore $\theta=\pm\frac{\pi}{4}\implies y=\pm x$
(This is essentially the same as Bernard's answer, but hopefully provides some intuition.)
First, recall the standard "little-$o$" notation: if we are interested in limits around $L$, then writing "$o(f(x))$" means "an omitted term $t(x)$ such that $\lim_{x\to L}{\frac{t(x)}{f(x)}}=0$." (Or, less precisely, "an omitted term much smaller than $f(x)$".) In our case, we'll be interested in limits around $0$, so $L=0$.
Now note that the definition of the derivative (or equivalently, Taylor's theorem) gives us an equivalent characterization of tangent lines:
The tangent line at the origin is $y=sx$ iff the original curve is $y=sx+o(x)$.
Tentatively assuming that a tangent line exists for some value of $s$, we can substitute this expression in for $y$ to obtain $$x(x^2+s^2x^2+o(x^2))=a(x^2-s^2x^2+o(x^2))$$ Expanding, $$(1+s^2)x^3+o(x^3)=a(1-s^2)x^2+o(x^2)$$ Dividing by $x^2$, $$(1+s^2)x+o(x)=a(1-s^2)+o(1)$$ Taking the limit as $x\to0$, any term that is $o(1)$, $\sim x$, or $o(x)$ vanishes. Thus $$0+0=a(1-s^2)+0$$ and we can see that the tangency slopes are $s=\pm1$.
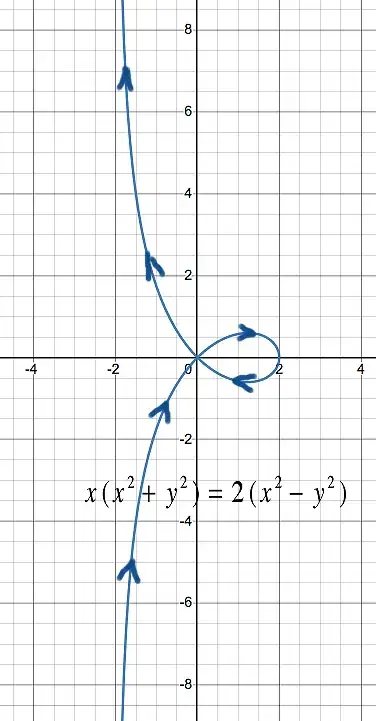
The appearance of an indeterminate implicit derivative at a point on a curve is often an indication of a self-intersection. This is a folium, the best-known example being that of Descartes $ \ ( x^3 + y^3 - 3axy \ = \ 0 ) \ , \ $ which looks like this one rotated counter-clockwise by $ \ 45º \ \ . $ We see that $ \ a \ $ "sets the scale" for the curve, with the "leaf" extending from the origin to $ \ x \ = \ +a \ $ and with a vertical asymptote located at $ \ x \ = \ -a \ \ . $
One way that the self-intersection can be investigated is by "parameterizing" the curve, introducing coordinate functions $ \ x \ = \ x(t) \ \ , \ \ y \ = \ y(t) \ $ which describe the curve in terms of a new independent variable ("parameter") $ \ t \ \ . \ $ (This approach is usually presented in second-semester calculus, so you may not have seen it when you posted your question). Because the curve is symmetric about the $ \ x-$axis, we would like the $ \ x-$coordinate to be given by an even-symmetry function of $ \ t \ . \ $ To avoid having a singularity at the origin, we also wish to have a function for the $ \ y-$coordinate with $ \ y(-\tau) \ = \ y(+\tau) \ = 0 \ $ and $ \ y(0) \ = \ 0 \ \ , \ \ x(0) \ = \ +a \ \ , $ so that the origin is "passed through" twice and the point with $ \ t \ = \ 0 \ $ occurs at the "tip of the leaf"; this would suggest that $ \ y(t) \ $ should have odd symmetry.
We can find such a parameterization if we take $ \ y \ = \ tx \ $ (a "slope parameterization", as this represents a line of slope $ \ t \ $ through the origin) and insert it into the curve equation: $$ x·(x^2 \ + \ [tx]^2) \ \ = \ \ a· (x^2 \ - \ [tx]^2) \ \ \Rightarrow \ \ x·(1 \ + \ t^2) \ \ = \ \ a \ - \ at^2 \ \ , \ \ x \ \neq \ 0 $$ $$ \Rightarrow \ \ x \ \ = \ \ a·\left(\frac{1 \ - \ t^2}{1 \ + \ t^2} \right) \ \ \Rightarrow \ \ y \ \ = \ \ tx \ \ = \ \ a·\left(\frac{t·(1 \ - \ t^2)}{1 \ + \ t^2} \right) \ \ . $$
We can (for now) generalize these coordinate functions a bit to fit the values of $ \ t \ $ we described above; thus, $$ x(t) \ \ = \ \ a·\left(\frac{\tau^2 \ - \ t^2}{\tau^2 \ + \ t^2} \right) \ \ , \ \ y(t) \ \ = \ \ -a·t·\left(\frac{\tau^2 \ - \ t^2}{\tau^2 \ + \ t^2} \right) \ \ . $$ The folium is "traced out" with the origin approached "from below" and near the vertical asymptote as $ \ t \ $ approaches $ \ -\tau \ $ from "negative infinity", the "leaf" is covered by $ \ -\tau \ < \ t \ < \ +\tau \ , \ $ then the origin is departed "from above" and near the asymptote as $ \ t \ $ "goes to positive infinity".
We already see that the conflict of derivatives at the origin is resolved by calculating the first derivative at two distinct values of the parameter:
$$ \frac{dy}{dx}|_{x \ = \ 0} \ \ = \ \ \frac{dy/dt}{dx/dt}|_{t \ = \ +\tau} \ \ = \ \ \frac{a·\left( \frac{t^4 \ + \ 4 \tau^2 · t^2 \ - \ \tau^4}{(\tau^2 \ + \ t^2)^2} \right)}{-a·\left(\frac{ 4 \tau^2 · t}{(\tau^2 \ + \ t^2)^2} \right)}|_{t \ = \ +\tau} $$ $$ = \ \ -\frac{ \tau^4 \ + \ 4\tau^4 \ - \ \tau^4}{4·\tau^3} \ \ = \ \ -\tau \ \ , $$
$$ \text{and} \ \ \ \frac{dy/dt}{dx/dt}|_{t \ = \ -\tau} \ \ = \ \ -\frac{ \tau^4 \ + \ 4\tau^4 \ - \ \tau^4}{4·[-\tau^3]} \ \ = \ \ +\tau \ \ . $$
Thus we can account for the two slopes of tangent lines with equal magnitudes and opposite signs at the origin, since the derivative $ \ \frac{dy}{dx} \ $ is the ratio of an even function to an odd function. (We also see that this correctly accounts for the vertical tangent at the end of the folium's "leaf", since the denominator becomes zero for $ \ t \ = \ 0 \ , $ making the derivative undefined.)
We still need to get the "scaling" of the curve set up properly. We can choose any point on the "leaf", say, $ \ x \ = \ \frac{a}{2} \ \ , $ for which $$ \frac{a}{2}·\left( \ \left[\frac{a}{2} \right]^2 \ + \ y^2 \ \right) \ \ = \ \ a·\left( \ \left[\frac{a}{2} \right]^2 \ - \ y^2 \ \right) $$ $$ \Rightarrow \ \ y^2 \ \ = \ \ \frac{a^3/8}{3a/2} \ \ = \ \ \frac{a^2}{12} \ \ \Rightarrow \ \ y \ \ = \ \ \pm \frac{a}{2 \sqrt3} \ \ . $$ Solving $ \ x(t) \ = \ \frac{a}{2} \ $ gives us $ \ t \ = \ \pm \frac{\tau}{\sqrt3} \ $ and inserting this into the other coordinate function yields $$ y \left(\pm \frac{\tau}{\sqrt3} \right) \ \ = \ \ -\left(\pm \frac{\tau}{\sqrt3} \right)· \frac{a}{2} \ \ = \ \ \pm \frac{a}{2 \sqrt3} \ \ \Rightarrow \ \ \tau \ \ = \ \ \mp 1 \ \ . $$ So the coordinate functions are "forced" to be $$ x(t) \ \ = \ \ a·\left(\frac{1 \ - \ t^2}{1 \ + \ t^2} \right) \ \ , \ \ y(t) \ \ = \ \ -a·t·\left(\frac{1 \ - \ t^2}{1 \ + \ t^2} \right) \ \ , $$ "tracing out the leaf" over the interval $ \ -1 \ < \ t \ < \ +1 \ . $ The slopes of the two tangent lines at the origin are thus $ \ \frac{dy}{dx}|_{x \ = \ 0} \ = \ \pm \ 1 \ \ . $
$$ \ \ $$
If we follow on Eric Tower's comment on the posted question by writing the two explicit functions which represent the portions of the curve that lie "above and below" the $ x-$axis, we have $ \ x(x^2 + y^2) = a(x^2 - y^2) \ \Rightarrow \ y^2 \ = \ x^2·\left(\frac{a - x}{a + x} \right) \ \ . $ When we perform explicit differentiation on these functions, we obtain $$ y' \ \ = \ \ \pm \left[ \ \left(\frac{a - x}{a + x} \right)^{1/2} \ + \ \frac12·x·\left(\frac{a + x}{a - x} \right)^{1/2} · \frac{2a}{(a - x)^2} \ \right] \ \ . $$ We needn't fuss with the expression further, as we see that for the two functions, $$ y'|_{x \ = \ 0} \ \ = \ \ \pm \left[ \ \left(\frac{a - 0}{a + 0} \right)^{1/2} \ + \ \frac12·0·\left(\frac{a + 0}{a - 0} \right)^{1/2} · \frac{2a}{(a - 0)^2} \ \right] \ \ = \ \ \pm \sqrt{\frac{a}{a}} \ \ = \ \ \pm 1 \ \ , $$ without any singularity in the calculation.