Finding smooth behaviour of infinite sum

Question

Define $$E(z) = \sum_{n,m=-\infty}^\infty \frac{z^2}{((n^2 + m^2)z^2 + 1)^{3/2}} = \sum_{k = 0}^\infty \frac{r_2(k) z^2}{(kz^2 + 1)^{3/2}} \text{ for } z \neq 0$$ $$E(0) = \lim_{z \to 0} E(z) = 2 \pi$$

where $r_2(k)$ is the number of ways of writing $k$ as a sum of two squares of integers. Is $E(z)$ smooth at $z = 0$, and can we evaluate its derivatives $(\partial_z)^n E(z)|_{z = 0}$?

---

_{Footnote 1: There is a physical motivation for these equations, $E(z)$ is the electric field generated by a $2d$ lattice of point charges where the lattice spacing is $z$ and the charge density is held fixed. $E(0)$ here is the continuum limit.}

_{Footnote 2: Here is a plot of the behavior of the sum in the second representation I wrote above from $k = 0$ to $k = N$, as a function of $z \in [-2,2]$. The black line is $2 \pi$. It looks like the limit will be very flat at $z = 0$ (possibly all derivatives vanish? That would be cool)}

Answer 1

§1. Basic results

We have to investigate the sum

$$E_s(z) = \sum_{n,m=-\infty}^\infty \frac{z^2}{((n^2 + m^2)z^2 + 1)^{3/2}}\tag{1.1}$$

Writing

$$\frac{z^2}{((n^2 + m^2)z^2 + 1)^{3/2}}=\int_{0}^{\infty} z^2 \sqrt{\frac{4 t}{\pi} }e^{-t(z^2 (m^2 + n^2) + 1)}\,dt\tag{1.2}$$

and doing the sums under the integral the double sum becomes this integral

$$E_i(z) = z^2 \int_0^{\infty}\sqrt{\frac{4 t}{\pi} }e^{-t} \vartheta _3\left(0,e^{-t z^2}\right)^2 \,dt\tag{1.3}$$

where $\vartheta _3$ is a Jacobi theta function.

This expression is better suitable to be plotted (using the NIntegrate command of Mathematica) than the sum.

Here is a picture of your function $E(z)$ for $z>0$ (for $z<0$ we have $E(-z)=E(z)$).

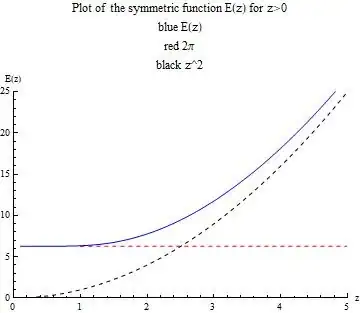
Notice that it is rather different from the plot in the OP.

Further results are:

For $z \to 0$ we have $E(z) = 2 \pi$, for $z>>1$ we have $E(z) \simeq z^2$.

All derivatives of $E(z)$ with respect to $z$ vanish for $z\to 0$ like $z^p e^{-1/z^2}$ (with some power $p$).

§2. Asymptotic expansions

Expanding the integrand $i(z,t)$ with respect to $z$ we obtain

1. for $z\simeq 0$

$$\begin{align}i = \frac{2\sqrt{\pi }}{\sqrt{t}} e^{-\frac{8 \pi ^2}{t z^2}-t} \left(2 e^{\frac{3 \pi ^2}{t z^2}}+e^{\frac{4 \pi ^2}{t z^2}}+2\right) \times\left(e^{\frac{3 \pi ^2}{t z^2}} \left(2-t z^2\right)+e^{\frac{4 \pi ^2}{t z^2}}+2\right)\end{align}\tag{2.1}$$

integrating over $t$ results in

$$\begin{align}E(0<z\simeq 0)=\pi \left(-e^{-\frac{2 \pi }{z}} \left(z^2+2 \pi z-8\right)-2 e^{-\frac{2 \sqrt{2} \pi }{z}} \\ \left(z^2+2 \sqrt{2} \pi z-4\right)-2 e^{-\frac{2 \sqrt{5} \pi }{z}} \left(z^2+2 \sqrt{5} \pi z-8\right)\\ +8 e^{-\frac{4 \pi }{z}}+8 e^{-\frac{4 \sqrt{2} \pi }{z}}+2\right)\end{align}\tag{2.2}$$

the leading terms of which are

$$\begin{align}E(0<z\simeq 0)=\pi \left(2 + 8 e^{-\frac{2 \pi }z}+ 8 e^{-\frac{4 \pi }z}\right)\end{align}\tag{2.3}$$

2. for $z\to \infty$

Developing first $\vartheta _3\left(0,e^{-u}\right)^2$ for $u\to \infty$ and then replacing $u \to t z^2$ we find for the integrand

$$i(z\to +\infty) \simeq \frac{2 e^{-t} \sqrt{t} z^2 \left(2 \left(e^{-4 t z^2}+e^{-t z^2}\right)+1\right)^2}{\sqrt{\pi }}\tag{2.4}$$

After integration over $t$ this leads to the interesting result

$$\begin{align}E(z\to \infty) \simeq z^2 \left(1+\frac{4}{\left(1+z^2\right)^{3/2}}+\frac{4}{\left(1+2 z^2\right)^{3/2}}\\ +\frac{4}{\left(1+4 z^2\right)^{3/2}}+\frac{8}{\left(1+5 z^2\right)^{3/2}}+\frac{4}{\left(1+8 z^2\right)^{3/2}}\right) \end{align}\tag{2.5}$$

Here the following two sequence of numbers appear: $\{0,1,2,4,5,8,...\}$ as a factor before $z^2$ in the denominator and $\{1,4,4,4,8,4,...\}$ in the numerator.

The first series (if prolonged by taking into account higher order terms) is easily identified in OEIS as A001481 Numbers that are the sum of 2 squares.

The second series is A004018 Theta series of square lattice (or number of ways of writing n as a sum of 2 squares). Often denoted by r(n) or r_2(n).

Hence the asymptotic form $(2.5)$ leads automatically to the second sum in the OP (the one containing $r_2(k)$)

Answer 2

Starting from the identity $$\left(1+a^2\right){\Large\mathstrut}^{\large-^3/_2} =\dfrac1{(1+a)^3}\left(1-\dfrac{2a}{(1+a)^2}\right){\Large\mathstrut}^{\large-^3/_2},$$ one can obtain high- accuracy approximation in the form of $$(1+a^2){\Large\mathstrut}^{\large-^3/_2} \approx\dfrac1{(1+a)^3} \left(1+\dfrac{3a}{(1+a)^2}+\dfrac{37a^2}{9(1+a)^4}+\dfrac{50a^3}{(1+a)^6}\right).\tag1$$

Assume $$t=\dfrac1z,\quad r=\sqrt{t^2+m^2},\tag2$$ then $$V(t)=E\left(\dfrac1t\right)=\sum\limits_{m,n\in\mathbb Z}\dfrac t{\left(t^2+m^2+n^2\right)^{\large^3/_2}} =\dfrac1{t^2}+2t\sum\limits_{m=1}^\infty \left(\dfrac 1{\left(t^2+m^2\right)^{\large^3/_2}} +2\sum\limits_{n=1}^\infty \dfrac 1{\left(t^2+m^2+n^2\right)^{\large^3/_2}}\right),$$

Since $$S_1(r)=\sum\limits_{n=1}^\infty (t^2+m^2+n^2){\Large\mathstrut}^{\large-^3/_2} =\dfrac1{r^3}\sum\limits_{n=1}^\infty\left(1+\left(\dfrac nr\right)^2\right)^{\large-^3/_2}$$ $$\approx \sum\limits_{n=1}^\infty\left(\dfrac1{(n+r)^3} \left(1+\dfrac{3rn}{(n+r)^2}+\dfrac{37r^2n^2}{9(n+r)^4}+\dfrac{50r^3n^3}{(r+n)^6}\right)\right)$$ $$=\dfrac1{181440}\bigg(225r^6\psi^{(8)}(r+1) + 5400r^5\psi^{(7)}(r+1) + 36764r^4 \psi^{(6)}(r+1) + 63168r^3 \psi^{(5)}(r+1) - 8400r^2 \psi^{(4)}(r+1) + 90720r \psi^{(3)}(r+1) - 90720 \psi^{(2)}(r+1)\bigg),$$ (see also Wolfram Alpha summation),

then $$V(t)=E\left(\dfrac1t\right) =\dfrac1{t^2}+2t\sum\limits_{m=1}^\infty \left(\dfrac 1{\left(t^2+m^2\right)^{\large^3/_2}} +2S_1\left(\sqrt{t^2+m^2}\right)\right).\tag3$$

Using the series representation near $\,m=\infty\,$ for each term under the sum, one can transform $(3)$ to the suitable series representation.

Answer 3

Here's another way to proceed. The Poisson summation formula tells us that summing the function over the lattice is the same as summing its fourier transform. Luckily, we can actually do the fourier transform: $$f(x) = \int_{\mathbb{R}^2} \frac{e^{-2 \pi i \langle y , x \rangle}z^2}{(y^2 z^2 + 1)^{3/2}} \mathrm{d}y = \int_\mathbb{R^2} \frac{e^{-2 \pi i v_1 x}z^2}{(v^2 z^2 + 1)^{3/2}} = 2\pi e^{-2\pi |x|/z}$$ where we have used the transformation of coordnates $v_1 = \frac{x_1 y_1 + x_2 y_2}{x}, v_2 = \frac{x_2 y_1 - x_1 y_2}{x}$ to do the first transformation, and then we can integrate over $v_2$ by trigonometric substitution, and over $v_1$ by picking out the residue in the top/bottom half plane of the countour integral.

Using this, we can explicitly write down the function as: $$E(z) = \sum_{k=0}^\infty 2\pi \ r_2(k) \ e^{-2\pi \sqrt{k}/z} = 2\pi + 8\pi e^{-2\pi/z} + 8\pi e^{-2\sqrt{2}\pi/z} + \dots$$ The 'problem' at $z=0$ in position space has been fixed, and it's clear to see now how all derivatives vanish at $z=0$.