Inverting an equation involving a sum of shifted functions

Question

I have the following system:

\begin{equation} f(x) = \sum_{n=-\infty}^{\infty} A_n(x-n x_0) g(x-nx_0) \end{equation}

where system functions $A_n(x)$ are known, and I am trying to express output $g(x)$ in terms of the input $f(x)$. We may assume that $A_n(x) = 0$ for $n > N$, such that the summation consists of finitely many terms. Also, the range of $x$ of interest can be restricted to a finite interval.

However, I am having trouble trying to invert the expression to determine $g(x)$. This is what I have attempted so far:

I suspect the answer will take the form

\begin{equation} g(x) = \sum_{n=-\infty}^{\infty} B_n(x) f(x+nx_0) \end{equation}

So, it looks like I want to determine what coefficients $B_n(x)$ are, and I believe these coefficients will be dependent only on the coefficients $A_n(x)$: If I change the input, I expect the output to change while $A_n(x)$ aren't changed. By symmetry in the target inverse expression, $B_n(x)$ should also not change, i.e. it is not dependent on the particular values of the input and output functions, but only dependent on $A_n(x)$. Please let me know if you think this assumption is incorrect.

By substituting one equation into another, we obtain

\begin{equation} f(x) = \sum_{j=-\infty}^{\infty}\sum_{k=-\infty}^{\infty} A_j(x-jx_0) B_k(x - jx_0) \, f(x -jx_0 + kx_0) \end{equation}

We can use the Kronecker delta to compact this equation into

\begin{equation} \sum_{j=-\infty}^{\infty}\sum_{k=-\infty}^{\infty} \Big(A_j(x-jx_0) B_k(x - jx_0) - \delta_{jk}\Big)\, f(x -jx_0 + kx_0) = 0 \end{equation}

$A_n(x)$ and $B_n(x)$ should not depend on the input, and so we can consider $f(x) = 1$ to get

\begin{equation} \sum_{j=-\infty}^{\infty}\sum_{k=-\infty}^{\infty} A_j(x-jx_0) B_k(x - jx_0) = 1 \end{equation}

This is as far as I've got, but I feel like an appropriate choice of $f(x)$ might reveal more relationships between $A_n(x)$ and $B_n(x)$ that would allow them to be solved.

Simpler(?) case

If the general problem cannot be practically solved, then the case I am particular interested in is when $A_n$ is constant for $n \ne 0$:

\begin{equation} f(x) = A_0(x) g(x) + \sum_{n \ne 0} A_n g(x-nx_0) \end{equation}

UPDATE

In the paper

Sandberg, H., & Mollerstedt, E. (2005). Frequency-domain analysis of linear time-periodic systems. IEEE Transactions on Automatic Control, 50(12), 1971-1983.

the concept of a Harmonic Transfer Function is used to relate functions of frequency that follow the same relationship as above. In the terms used in the question, an infinite dimension vector is defined, whose elements consist of a function that is incrementally shifted as one goes down the vector:

\begin{equation} \mathbf{f}(x) = \begin{bmatrix} \dots & f(x+2x_0) & f(x+x_0) & f(x) & f(x-x_0) & f(x-2x_0) & \dots \end{bmatrix}^T \end{equation}

\begin{equation} \mathbf{g}(x) = \begin{bmatrix} \dots & g(x+2x_0) & g(x+x_0) & g(x) & g(x-x_0) & g(x-2x_0) & \dots \end{bmatrix}^T \end{equation}

That is, we have vectors whose elements are defined as $f_n(x) = f(x-nx_0)$, and $g_n(x) = g(x-nx_0)$, where $-\infty < n < \infty$.

Therefore, we can express the following:

\begin{equation} f_j(x) = \sum_{j = -\infty}^{\infty} A_{jk}(x) g_k(x) \end{equation}

where $A_{jk}(x) = A_{k-j}(x-kx_0)$. That is, we an infinite linear matrix equation:

\begin{equation} \mathbf{f}(x) = \mathbf{A}(x) \mathbf{g}(x) \end{equation}

Now, this looks like something we can invert:

\begin{equation} \mathbf{B}(x) = \mathbf{A}^{-1}(x) \quad\text{such that}\quad \mathbf{g}(x) = \mathbf{B}(x) \mathbf{f}(x) \end{equation}

where $B_{jk}(x) = B_{j+k}(x-jx_0)$.

However, we have two problems: the matrix elements are functions of $x$, and the vectors and matrix are of infinite dimension! Is there a practical way to invert an infinite matrix, and would the inversion need to be done separately for each individual value of $x$? I get the feeling it might be possible to choose a matrix that is large enough, and it would be sufficient to invert that.

Numerical example

For the simplest case where $A_n(x) = A_n$ (i.e. constant), then $A_{jk} = A_{k-j}$. Let's consider the following example:

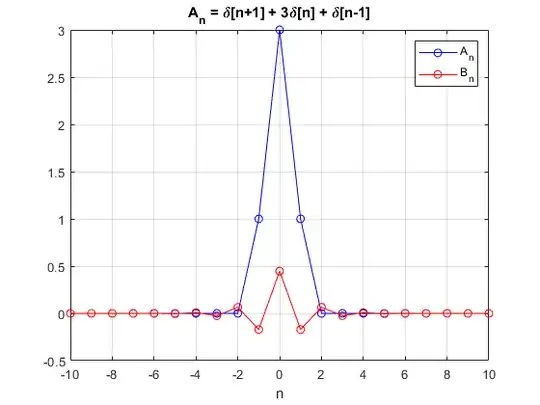
\begin{equation} A_n = \delta[n+1] + 3\delta[n] + \delta[n-1] \end{equation}

where

\begin{equation} \delta[n] = \begin{cases} 1 & \text{for $n=0$}\\ 0 & \text{for $n\ne 0$}\\ \end{cases} \end{equation}

That is,

\begin{equation} f(x) = g(x-x_0) + 3g(x) + g(x+x_0) \end{equation}

I obtain matrix $\mathbf{A}$, but I truncate it to a $201 \times 201$ matrix with the index ranging in $-100 \le n \le 100$.

Then I take the inverse of the matrix, and I extract the row at index $n=0$, which is $B_{0n} = B_n$. Using MATLAB to perform this inverse, I get

\begin{equation} B_{n} = \dots + 0.0652\delta[n+2] - 0.1708\delta[n+1] + 0.4472\delta[n]\\ - 0.1708\delta[n-1] + 0.0652\delta[n-2] + \dots \end{equation}

In other words,

\begin{equation} g(x) = \dots + 0.0652f(x + 2x_0) - 0.1708f(x + x_0) + 0.4472f(x)\\ - 0.1708f(x - x_0) + 0.0652f(x - 2x_0) + \dots \end{equation}

This appears to be what I want. Furthermore, it seems to show no discernible change whenever I increase the size of the matrix at truncation.

This is good, but I feel like this is still going to be quite clunky for the case where $A_0(x)$ is a function while $A_n$ is constant for $n \ne 0$. I don't want to have to invert a matrix for every value of $x$! Is there a way to extend the above numerical case to this slightly more complex case?

Aside

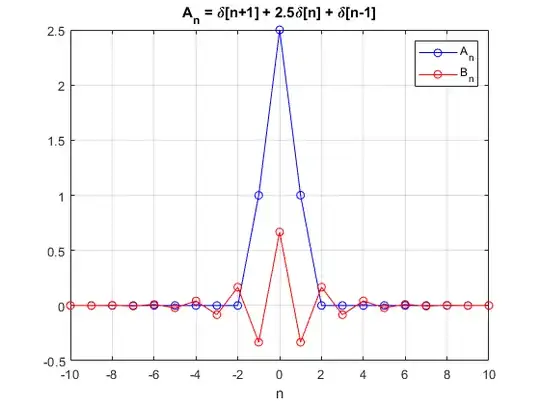
Interestingly, if I change the value of $A_0$ from 3 to a different value $m$, we get some interesting behaviour...

For $m = 2.5$:

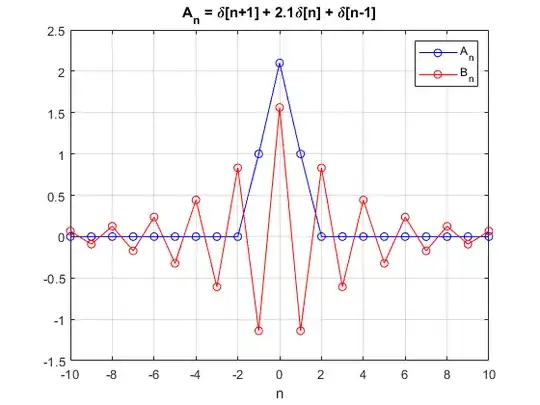
we see how the $B_n$ coefficients remain large over a larger span of index $n$. This is particularly noticeable for $m=2.1$:

As long as the coefficients drop off to zero before getting to the "edge" of the matrix, I think it is reasonable to assume these coefficients are the inverse that I'm looking for. However, for $m=2$, the coefficients do not die down sufficiently fast, only reaching zero right at the edge, and we see that the height of the coefficient $B_0$ is on the order of the size of the matrix:

If fact, $B_0$ seems to scale in proportion to the size of the matrix, suggesting that the untruncated infinite matrix would cause $B_n$ to blow up to infinity. This suggest certain systems of equations are singular, and cannot be inverted...

Answer 1

Very interesting problem and thanks for posting it!

This problem as posted is too general and multifaceted to solve completely but I hope that with this answer I will cover the case of interest and at the very least elucidate the nature of the problem and explain what is happening with the numerics.

The general form of the problem can be written

$$g(x)=\sum_{n=-\infty}^{\infty}A_n(x)f(x-nx_0)$$

and our desire is to express $f(x)$ explicitly in terms of $g(x), A_n(x)$.

First, let us solve the simplest case, where $A_n(x)\equiv A_n$ are constants. As noted in the question above, one strategy to solve for $f$ (at least when only a finite number of $A_n$'s are non-zero) is to write down the translates of the equation defining $f$ and start eliminating variables leaving only $f(x)$ on the right hand side. This is basically the inversion procedure for an infinite Toeplitz matrix. There are at least 3 different ways to proceed with the elimination procedure which I will dub forward, backward and symmetric propagation (in the examples provided in the OP symmetric elimination is used). As an example, consider

$$A_n=\delta_{n+1}+\delta_{n-1}+3\delta_n$$

Denote $g(x+nx_0):=g_n$ and $f(x+nx_0):=f_n$. One may wish to write the first few equations symmetrically around $n=0$ like so

\begin{align} &g_1=f_2+3f_1+f_0\\ &g_0=f_1+3f_0+f_{-1}\\ &g_{-1}=f_0+3f_{-1}+f_{-2} \end{align}

Here we can only eliminate two variables between the 3 equations, and the only variables eligible for that are $f_1, f_{-1}$, leaving the outermost $n$ values, as well as the desired $n=0$. To approximately solve for $f$ we can arbitrarily apply the absorbing boundary condition $f_2=f_{-2}=0$, and then write the problem in the linear algebra form

$$\begin{pmatrix}g_{-1}\\g_0\\g_1\end{pmatrix}=\begin{pmatrix}0&1&3\\1&3&1\\3&1&0\end{pmatrix}\begin{pmatrix}f_{-1}\\f_0\\f_1\end{pmatrix}$$

We may strategize similary for forward propagation, instead choosing to only consider $n>0$ translates, as in the following set of equations

\begin{align} &g_1=f_2+3f_1+f_0\\ &g_2=f_3+3f_2+f_{1}\\ &g_3=f_4+3f_{3}+f_{2} \end{align}

where we can eliminate the inner variables $f_1, f_2$ and keeping the outermost $f_3, f_4$. Truncating with an absorbing boundary to approximate the solution yields the equation

$$\begin{pmatrix}g_{1}\\g_2\\g_3\end{pmatrix}=\begin{pmatrix}1&3&1\\0&1&3\\0&0&1\end{pmatrix}\begin{pmatrix}f_{0}\\f_1\\f_2\end{pmatrix}$$

which can be solved for $f_0$. Backward propagation can be obtained by substituting $n\to -n$. From this analysis it should be evident that an approximate solution to the problem is always attainable, for any set of $f,g, A_n$. The reason why all these techniques are important is because all of them lead to a formal solution to the problem through slightly different techniques.

Given that the problem admits solutions under no condition makes manipulations using tools like generating functions and integral transforms restrictive, but note that the solutions obtained via formal versions of these tools provide the right answers for any choice of the functions.

Taking a formal version of the Fourier transform on both sides of the defining equation we see that

$$\hat{g}(\omega)=\left(\sum_{n=-\infty}^{\infty}A_n e^{-in\omega x_0}\right)\hat{f}(\omega):= R(\omega)\hat{f}(\omega)$$

The Fourier series representation of $R(\omega)$ with period $T=2\pi/x_0$ has to be non-zero in the interval $(0,T)$ or the problem is singular and it cannot admit a solution for any function $g$. Assuming the truth of this statement, we see that $1/R(\omega)$ is also $T$-periodic and therefore it also admits a Fourier series representation. Assuming henceforth that $1/R(\omega)=\sum_{k=-\infty}^{\infty} C_k e^{ik\omega x_0}$ we find that the solution to the problem can be written simply as

$$f(x)=\sum_{n=-\infty}^{\infty}C_n g(x+nx_0)~~,~~ C_n=\frac{1}{2\pi}\int_{-\pi}^\pi\frac{e^{-in\omega}}{R(\omega/x_0)}d\omega$$

whenever the series converges and $\lim_{x\to \infty} f(x)=\lim_{x\to \infty} g(x)=0$, but I have not worked to specify the most general conditions under which this holds. Modifications are certainly necessary, by considering the function $g(x)=e^x$ with the coefficients from the example above, in which case $f$ and $g$ both diverge as $x\to\infty$ and one must take the limit of infinite equations carefully.

To apply this to the numerics above, note that in the aforementioned example $R(\omega)=e^{-i\omega}+3+e^{i\omega}$ and we can explicitly compute the Fourier coefficients

$$C_n=\frac{(-1)^n}{\sqrt{5}}\left(\frac{3-\sqrt{5}}{2}\right)^{|n|}$$

which matches the numerics provided. This formula also explains why the coefficients diverge in the example with $R(\omega)=e^{-i\omega}+2+e^{i\omega}=4\cos^2(\omega/2)$, which has zeros located at $\omega=\pm\pi$. This indicates that this particular symmetric propagation problem may not have a solution, but further investigation with Mathematica shows that there may be a way to obtain the coefficients for any truncation level using a regularized version of the Fourier series (I will not go into this right now).

We can finally work on the solution of the more general problem where all the $A_n$'s are constant except for $A_0$. We take the Fourier transform formally one more time and we see that

$$g(\omega)=\left(\sum_{n\neq 0} A_n e^{-in\omega x_0}\right)\hat{f}(\omega)+\int_{-\infty}^\infty \hat{A}_0(\omega-\omega')\hat{f}(\omega')\frac{d\omega'}{2\pi}$$

This is a Volterra integral equation of the 2nd kind and it can be solved using iterative techniques:

$$\hat{f}(\omega)=\frac{\hat{g}(\omega)}{R(\omega)}-\int \frac{\hat{A}_0(\omega-\omega_1)}{R(\omega)}\frac{g(\omega_1)}{R(\omega_1)}\frac{d\omega_1}{2\pi} +\int\frac{\hat{A}_0(\omega-\omega_1)}{R(\omega)}\int \frac{\hat{A}_0(\omega_1-\omega_2)}{R(\omega_1)}\frac{g(\omega_2)}{R(\omega_2)}\frac{d\omega_1 d\omega_2}{(2\pi)^2}-...$$

which after performing the inverse Fourier transform gives the surprisingly neat formula

$$f(x)=\sum_k C_k g(x+kx_0)-\sum_{kl}C_k C_l A_0(x+kx_0)g(x+(k+l)x_0)+\sum_{klm}C_k C_l C_m A_0(x+kx_0)A_0(x+(k+l)x_0)g(x+(k+l+m)x_0)-...$$

A bit more work is needed in this case to extract coefficients but it's fairly easy to see that with $f(x)=\sum_{n}B_n(x)g(x-nx_0)$

we find

$$B_n(x)=C_n-\sum_k C_k C_{n-k}A_0(x+kx_0)+\sum_{kl} C_k C_l C_{n-k-l}A_0(x+kx_0)A_0(x+(k+l)x_0)-...$$

It seems as though this technique is enough to solve the most general problem as well, albeit in not very pretty or illuminating form.

There's more to be said about forward/backward propagation and obtaining solutions in terms of Taylor expansions but I will write something about it only if there's interest.